By Josh Feldman
With the pandemic going on far longer than anyone had imagined, our local gang used to meet at The Gardens in town so we could see each other in a socially distant way while keeping in touch. Alas, with cold weather and snow hitting the area, recently our outdoor meetups have been abandoned, instead replaced by Zoom calls.
It seems like every Zoom call is the same as we all just reminisce about what life would be like in normal times. We all go back and forth talking about what we will do once this is all over and done with. Amazingly, a lot of us in the group really miss one thing: local road races. All of us desperately look forward to lacing up our racing flats and competing against one another again. This is especially true because the last race we competed in left a sour, sour taste in our mouths…
It seems like every city in America has a local legend that dominates the running scene in town, and where I live—Columbia, Missouri—is no different in that regard. While in most cities the top dog is well-respected, in Central Missouri it is the exact opposite. The fastest runner here is named Bathalsador, and without exception everyone despises the guy with a passion. And in the late 2020 February road race, Bathalsador gave everyone even more reasons the loathe him.
On race day that February morning 12 months ago, to the relief of everyone, no one saw Bathalsador (or “Batty,” as the locals call him) on the starting line. As we all lined up to start the race, we all prayed that Batty slept in and wouldn’t participate. But our prayers would not get answered that day. Unbeknownst to us, instead of starting at the front of the pack, Batty lined up with last row of competitors.
When the gun sounded and the race began, Batty sprinted up to us leading the race. Then, instead of continuing to pass us (which would have been acceptable), Batty did his grandstanding act, quickly turned a 180, and sprinted back to the final row of competitors. I have no idea how he managed to avoid everyone running in the opposite direction, but fortunately he did so. Finally, after reaching the last row of competitors, Batty did another 180-degree turn, and started racing for real. Alas, even with the extra distance covered, Batty still easily won the race. If only one of us had the talent to put Batty in his place once and for all and win the race. But on that day, it just wasn’t in the cards.
A few minutes after the race, someone asked me: “How much longer did Batty run than the rest of us?” I honestly had no clue. But maybe we with a little luck and a little math we could figure it out.
I overheard a few others who lined up next to Batty in the back row say that when Batty made his second and final 180-degree turn, they just crossed the starting line (where the first row of competitors originally lined up). Further, our friends in the back row said it was exactly 150 meters from where they lined up to where I was in the front row.
While the “back row gang” of runners may not be the most talented runners on earth, they race their tails off, and I know that for at least the first half mile of the race they run at the exact same pace as those of us who comprised of the front row. You would think with all of this information I could tell everyone how much farther Batty ran than all of us, but I was in no mood to solve the problem. For those of you that haven’t tried it, it’s darn tough to do math problems after a hard run! Fortunately, I have my Contingencies puzzle friends who can solve the problem for us.
Given that Batty lined up 150 meters behind us in the front row and pulled off the stunt described above (feel free to assume it took Batty no time to change directions, Batty ran at the same speed for the entire race, and that all the other runners in the race ran at a constant speed for the first part of the race), how much farther did he run compared to us in the front row?
Special thanks to Allan Gottlieb who helped provide massive inspiration for this puzzle!
Solutions to Last Issue’s Puzzle
A Crossnumber Puzzle with Squares
Problem: Fill in the following 4×5 rectangle with the digits 0 to 9 satisfying the given conditions.
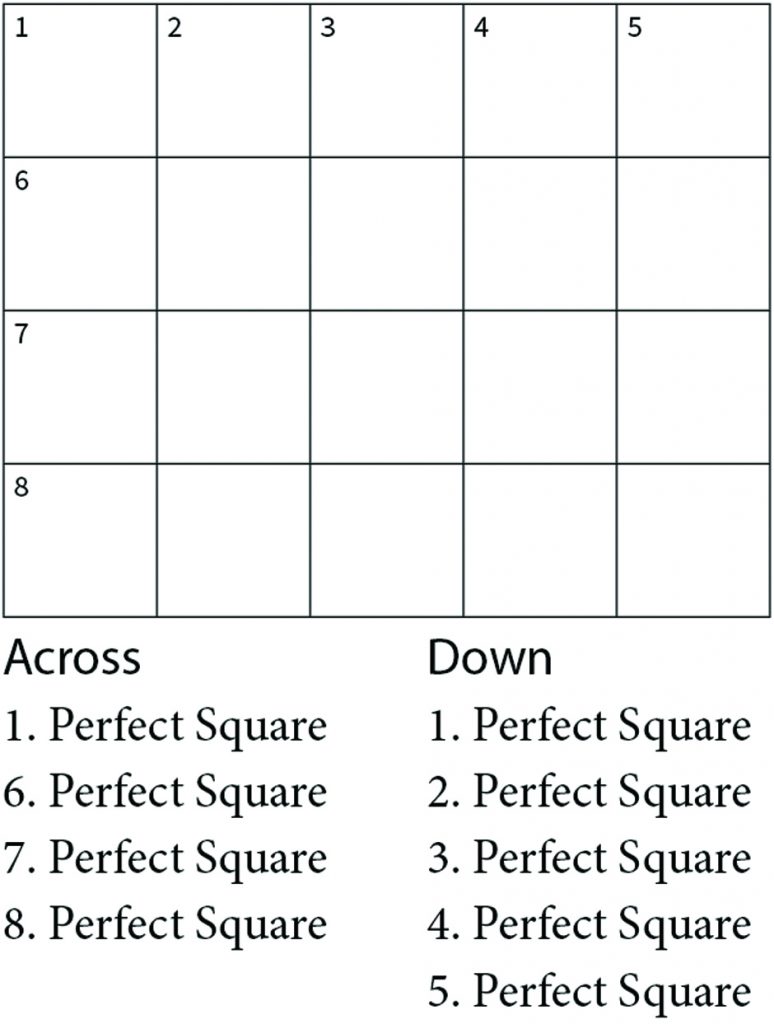
All 9 entries, 4 rows plus 5 columns, are different numbers, where 0016 and 00016 are the same number.
There are 100 answers to this crossnumber problem, so additional conditions were added.
Problem 1: Find an answer with 1 Across = 00000. Two of the 6 answers are {0, 7, 10, 140} and {0, 1, 152, 238}. All answers will be shown by listing the square roots of their four rows from top to bottom.
Problem 2: Find an answer with 1 Down = 0000. Two of the 20 answers are {1, 4, 20, 70} and {70, 3, 96, 81}.
Problem 3: Find an answer with 4 Down = 0000. Two of the 18 answers are {20, 100, 30, 98} and {20, 100, 70, 98}.
Problem 4: Find an answer with one of the other 6 entries = 0000 or 00000. Two of the 13 answers are {1, 14, 200, 300} and {142, 157, 0, 300}.
Problem 5: Find an answer where the 2×3 rectangle in the upper left corner and the 2×2 square in the lower right corner are all 0s. Two of the 22 answers are {0, 7, 10, 140} and {6, 8, 290, 140}.
Problem 6: Find an answer with 2×2 and 2×3 interchanged in the prior problem. One of the 2 answers is {1, 14, 200, 300}.
Problem 7: Find an answer which contains 14 0s. One of the 14 answers is {0, 7, 10, 140}.
Problem 8: Find an answer where none of the nine entries has leading 0s. The unique answer is {131, 152, 172, 238}. [Source: Problem 8 is Problem 68 in the new problem book by Bernardo Recamán: The Bogotá Puzzles. Communicated to me by Stan Wagon. Problems like this have been floating around since at least 1999. Who knew? I thought I invented them two years ago.]
Solutions
Answers for all or most of the first seven problems might be found by “fiddling around” to use a technical term. However, problem 8 is too hard to do that way. When I asked solvers how they solved that problem, many of them said they used “brute force.” However, after probing deeper, I discovered a few interesting varieties of brute force. One thing many did was to first find the 100 answers to the basic crossnumber problem and then they selected the answers to the eight subproblems from those 100. The latter could be done by observation, an Excel program, or something similar.
I will focus on the first part. No one was naïve enough to try to test all 1020 distinct digit filled 4×5 rectangles. However, one approach that was used was to test all rectangles where the rows consisted of 4 distinct 5-digit squares from the set 02 to 3162, i.e. 00000 to 99856. There are 9,908,012,520 such rectangles. For each rectangle one needs to check whether the 5 columns are squares, distinct from each other, and distinct from the rows; about 20 operations per rectangle. As reported, that took about 4 days using APL.
(Using 5 columns of distinct 4-digit squares instead of 4 rows of 5-digit squares, there are only 9,034,502,400 rectangles to check and fewer operations are needed to check them, which should reduce the run-time by about 10%.)
A more efficient approach would be to consider that the last digit of a square cannot equal 2,3,7, or 8. This significantly reduces the number of rectangles to check but increases the sophistication of the programming.
Going even further, one could focus on the digit in the bottom right corner and build answers from there. In this way, the work could all be done by hand. The number of the 100 basic answers by corner digit is {47,10, 0, 0, 23, 0, 8, 0, 0, 12}. from 0 to 9 respectively. The interesting numbers here are 47 for 0, where all 4 digits in the bottom right corner are 0 and 0 for 5.
Solvers
Welcome to the list, Susan Poole, Adam Roesch, and Jacob Sundberg.
Also, Robert Bartholomew, Bob Byrne, Samantha Casanova, Andrew Dean, Bill Feldman, Rui Guo, David Kausch, Clive Keatinge, Alex Kozmin, David Promislow, Noam Segal, Tomasz Serbinowski, John Snyder, Al Spooner, Daniel Wade.





