By Josh Feldman
As if running on New Orleans streetcar tracks isn’t dangerous enough, a new, darker, more treacherous phenomenon has taken America by storm. Of course, I am talking about the new Netflix show Squid Game, easily the best television show of the year (and I say this as someone who watches more than my share of TV). As if 18 months of a pandemic didn’t set everyone on edge, we now have a new hobby in this ingenious life-or-death game. Thanks to the show, people throughout our land suddenly think differently about simple childhood games.
For those of you unfamiliar with Squid Game, feel free to stop reading this column now and watch all nine episodes of Season 1. And make sure the little ones aren’t around when you do watch, as this is without a doubt a show for grownups only (don’t say I didn’t warn you)! I promise this puzzle will still be around after you complete the binge viewing!
One of the things that makes this show so great are the decisions, both big and small, that everyone must make throughout the show. There are of course the big decisions, like whether you should play the game or walk away, and the small yet incredibly consequential decisions, like which shape you should choose, or where to stand in line during a game. What is great about the show is that no matter how trivial the decision appears to be, you know it will quickly have an unknown, maximal impact. Every choice has life-or-death results, and every time a possibility arises, you know it will be important.
Of course, whenever there are options, frequently math is present, directly or indirectly in the background. And that is exactly what we saw in one of the later episodes of the show.
In the devious glass game played in the seventh episode of the series, contestants have 10 minutes to cross a bridge of 16 steps. For each step, the player has a choice to pick the left pane or the right pane. In each case, one of the two panes randomly contains normal glass, which will quickly break when stepped upon. The other mirror contains tempered glass, which one can safely step on without breaking. The bad news is that if the glass breaks, the competitor falls to his/her untimely demise. The good news is that the sacrifice is not for naught, as this pane no longer exists, giving all the remaining contestants valuable information as to what the correct path to safety is. Each competitor attempts to cross the bridge in order and continues moving until the player either successfully crosses all 16 steps on the bridge or literally dies trying.
While watching the show with my brother, he asked me: What is the probability of the 12th player—my brother’s favorite character—making it across the bridge safely? I told him that I didn’t know off the top of my head, but I bet my puzzle-solving friends could help him out!
Make the following assumptions.
a. There are 18 players.
b. The bridge has 16 steps, each of which has a left- or right-side pane.
c. There is a 50% chance that the left pane of each step has tempered glass, and if the left side has tempered glass, the right side does not (and vice versa).
d. It is impossible to tell the difference between the normal and tempered glass.
e. None of the contestants make any mistakes (so if the first contestant chooses to go left on the first pane and safely steps on tempered glass, all the remaining players see that they need to choose the left mirror for step 1).
Problems:
- What is the probability that each of the 18 players makes it safely across the bridge?
- How would these probabilities change if players didn’t see the above players in line perform, but could still see the broken / deadly panes of glass previous contestants left behind?
Note: Ronald Stokes correctly answered the streetcar puzzle from two issues ago, and we accidentally left his name off the solvers list.
Solutions may be emailed to cont.puzzles@gmail.com. In order to make the solver list, your solutions must be received by December 1, 2021.
Previous Issue’s Puzzle—Multigraphs
There are 4n pebbles of weights 1, 2, 3, … , 4n. Each pebble is colored one of n colors and there are 4 pebbles of each color.
Problem 1
How many ways are there of coloring the 4n [distinct] pebbles using n colors with 4 pebbles of each color when n = 3 (12 pebbles) and when n = 4 (16 pebbles)?
- Answer: 5,775 for n=3 and 2,627,625 for n=4.
- Solution: The general formula is (4n)!/(n!(4!)n)
Alternatively, one can observe that for n =2, once the color for pebble 1 is selected there are C(7,3) =35 ways of choosing the remaining 3 pebbles of that color, as was mentioned in the writeup. It doesn’t matter that pebble 1 could have been another color; we are only concerned about color differences. For n=3, there are C(11,3)=165 possible sets of associates of pebble 1, leaving 8 pebbles to be split into 2 colors—which is just the n=2 case. So, for n=3 the answer is 165×35. Similarly, for n=4 the answer is C(15,3)=455 times 5,775.
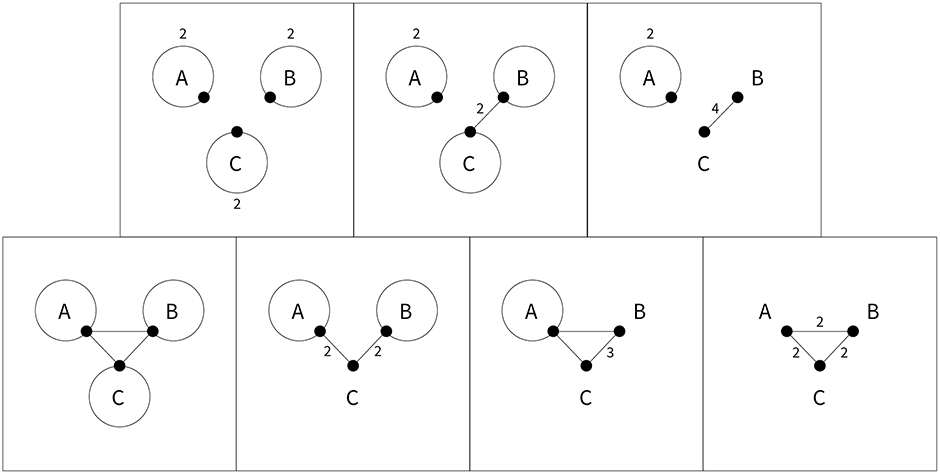
Problem 2
Find the 7 multigraphs on three vertices with four edges at each vertex and use them to solve the problem[1] for n=3.
- Answer: The 7 multigraphs on three vertices are shown in Figure 2. (Figure 1 refers to the original problem writeup.) The multigraphs can be characterized by the number of loops at each vertex: (2,2,2), (2,1,1), (2,0,0), (1,1,1), (1,1,0), (1,0,0), (0,0,0). (Thanks to Gary Wang for this notation.) Multigraphs for the first three triples correspond to a two-loop vertex added to the multigraphs in Figure 1.
The second part of this problem asks for the solutions (pairs of piles) corresponding to each multigraph. Here are the piles for each multigraph:
- For (2,2,2), they are {AA, BB, CC} & {AA, BB, CC}.
- For (2,1,1), they are {AA, BC, BC} & {AA, BB, CC}.
- For (2,0,0), they are {AA, BC, BC} & {AA, BC, BC}.
- For (1,1,1), they are {AA, BB, CC} & {AB, AC, BC}.
- For (1,1,0), they are {AA, BC, BC} & {CC, AB, AB}.
- For (1,0,0), they are {AA, BC, BC} & {AB, AC, BC}.
- For (0,0,0), they are {AB, AC, BC} & {AB, AC, BC}.

Problem 3
How many multigraphs on four vertices with four edges at each vertex are there?
- Answer: 20
- Solution: Finding each of the 20 was a fun exercise, for me. Here are some hints if you want to look for them for yourself. You can get 7 by adding a two-loop vertex
to each of the multigraphs in Figure 2. You can get 3 more by combining the 2nd and 3rd multigraphs for n=2 from Figure 1. The remaining multigraphs are each connected; there are 10 of them. Using the number loops by vertex, there are 5 possibilities; the 10 multigraphs are distributed as follows: 1 with (1,1,1,1), 1 with (1,1,1,0), 3 with (1,1,0,0), 2 with (1,0,0,0) and 3 with (0,0,0,0). Alternatively, there are five underlying shapes of the multigraphs (with loops and duplicate edges deleted). The 10 connected multigraphs are distributed among the five underlying shapes as indicated in Figure 3.
Advice to multigraph hunters: 1) Sometimes pictures that look different are really the same multigraph. 2) How can you tell if you have all the multigraphs on n vertices? Write down n equations in n(n+1)/2 unknowns. One equation for each vertex and one unknown for each possible line, including loops. And then add appropriate restrictions. In our case, the right side of each equation is 4, and the unknowns are restricted to integers from 0 to 4, the loop unknowns are further restricted to either 0 or 1. (2 would correspond to a two-loop vertex added to a multigraph on n-1 vertices.) Using further restrictions, one can proceed on a case-by-case analysis. This process will find all the multigraphs, but you are likely to get many duplicates. 3) How can you tell if you have duplicates, once you’re sure you have them all. OEIS A129429 shows that the “number of isomorphism classes of 4-regular multigraphs of order n, loops allowed” is 1, 3, 7, 20, 54, … for n = 1, 2, 3, … (“4-regular” means 4 edges at each vertex and “order n” means n vertices.)
Notes on Solutions. Solutions presented here are not unique in many ways. What is presented is an (easy) pairing up algorithm to solve the problem stated. Even for n = 2, there are solutions that do not fit the algorithm and there are even multiple ways to implement the algorithm. And for n = 4, there are some multigraphs for which different solutions (or algorithms) can be implemented. Finally, it is interesting to look back at the distribution of the 35 colorings over the 3 multigraphs for n = 2. It is 3, 24, 8. For n = 3, the distribution is 15, 360, 120, 960, 1440, 1920, 960.
Solvers
Robert Bartholomew, Rui Guo, Clive Keatinge, David Promislow, Dan N. Ropp, Michael Schachet, John Snyder, and Gary Wang.
References
[1] “The problem” referred to here is to arrange the pebbles into two piles, so that the total weight of each pile is the same and each pile contains two pebbles of each color. We transformed this problem into creating a multigraph for each coloring and then creating the piles from the multigraphs. Capital letters represent distinct colors and vertices. Pairs of capital letters represent edges.




