By Stephen Meskin
I came across the following interesting problem from the 61st Annual International Mathematical Olympiad (IMO), which was held remotely on Sept. 20 & 21, 2020. The IMO is the world’s leading mathematical competition for high school students.
“There are 4n pebbles of weights 1, 2, 3, …, 4n. Each pebble is colored one of n colors and there are four pebbles of each color. Show that we can arrange the pebbles into two piles, so that the total weight of both piles is the same and each pile contains two pebbles of each color.”[1]
Of course, there is no problem when n = 1. When n = 2, there are eight pebbles, which can be colored using two colors with four pebbles of each color in 35 different ways. (Just consider how many ways the three pebbles with the same color as the pebble of weight 1 can be selected.) Thirty-five cases can be handled without much difficulty, but the number of colorings and difficulty increases dramatically as n increases.
Problem 1
How many ways are there of coloring the 4n pebbles using n colors with four pebbles of each color when n = 3 (12 pebbles) and when n = 4 (16 pebbles)?
To reduce the difficulty, we will transform the problem and, in the process, simplify it. Going back to the case n = 2, we pair the pebbles so that the sum of the weights of the pebbles in each pair is 9. The (unordered) pairs are (1,8), (2,7), (3,6), (4,5). So doing makes creating two piles with equal sums very easy; each pile need only contain any two pairs, thus allowing us to ignore the weights.
To solve the problem we only need to get exactly two of each color in each pile. Let the two colors be A and B and list each pebble by its color. Each pair can have only one of three colorings: (A, A), (B, B), (A, B). A coloring of the eight pebbles with four pebbles of each color then corresponds to a set of four pairs selected from these three with a total of 4 As and 4 Bs. There are only three such sets rather than 35: {(A, A), (A, A), (B, B), (B, B)}, {(A, A), (A, B), (A, B), (B, B)}, and {(A, B), (A, B), (A, B), (A, B)}. Each set leads to a solution; the three solutions are:
- Pile 1 {(A, A), (B, B)} Pile 2 {(A, A), (B, B)}
- Pile 1 {(A, A), (B, B)} Pile 2 {(A, B), (A, B)}
- Pile 1 {(A, B), (A, B)} Pile 2 {(A, B), (A, B)}
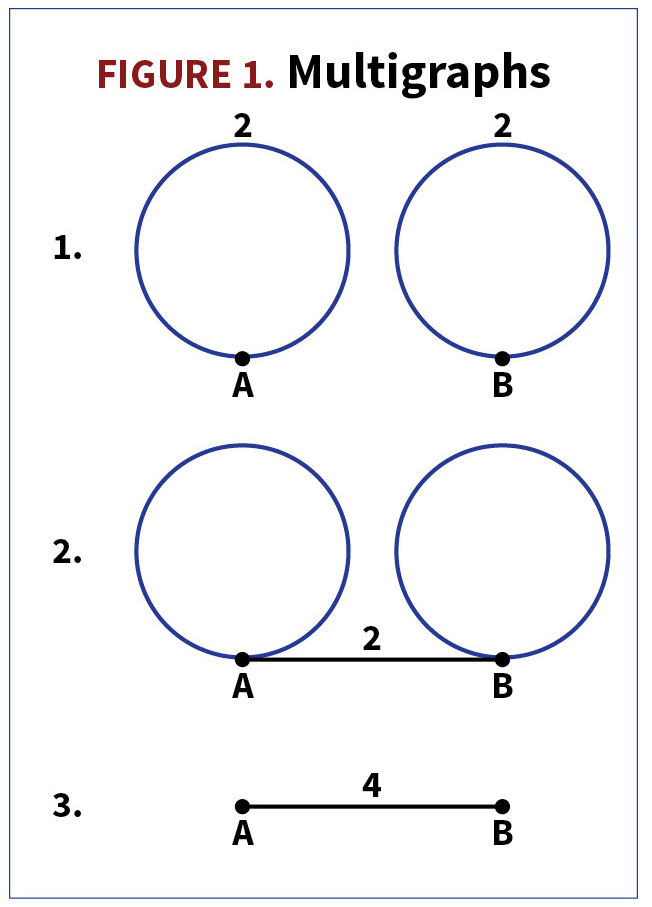
Now that’s easy! What I find more interesting than the solutions is that the colorings can be represented as multigraphs by taking each color to be a vertex and each pair in the set as an edge connecting two vertices, or a vertex with itself. (It is a multigraph because multiple edges can connect the same two vertices and because a vertex can be connected to itself.) For n = 2, the three sets become the multigraphs shown in Figure 1.
(A number on an edge indicates multiple edges.)
The characteristic of the multigraphs that corresponds to our problem is simply that the number of edges at each vertex is four (an edge connecting a vertex with itself is counted twice at that vertex).
Problem 2
Find the seven multigraphs on three vertices with four edges at each vertex and use them to solve the problem for n = 3.
Problem 3
How many multigraphs on four vertices with four edges at each vertex are there?
[Note: Problems 2 and 3 yield solutions to splitting up the pebbles into two piles for small n. The IMO problem only asked to show that such splittings exist, not how to find them, but asked it for all n].Solutions may be emailed to cont.puzzles@gmail.com.
In order to make the solver list, your solutions must be received by October 1, 2021.
SOLUTION to Previous Puzzles: City of New Orleans
Given that you run 8 mph, streetcars move at 10 mph, there are on average 10 times an hour you need to switch tracks to avoid the streetcar, and you need 0.02 miles of leeway every time you switch tracks, what is the probability of a sticky situation occurring in your hour long run?
Solution: Note, as a few people made slightly different assumptions, a few different answers were given full credit. If you run 10 mph, relative to the runner streetcars in the opposite direction come at you at 18 mph, while streetcars in the same direction move at 2 mph. Therefore, streetcars in the same direction come two-eighteenths as often as those coming in opposite direction of the runner. This means that during an hourlong run, you should expect on average (10 × 2)/18 = 1.1111 times during a run that a streetcar going the same direction as you passes you.
Each time a streetcar goes by you in the opposite direction, you spend 0.02 miles on the opposite track. As this happens on average 10 times an hour, for 0.02 × 10 or 0.2 miles the runner has to run on the opposite-side streetcar track during a typical run. As you run for 8 miles, this is (0.2/8), one-fortieth of the time you spend on the opposite side of the track on average during a run. Hence, a sticky situation occurs with an approximate probability of (1/40) × (10/9), or 2.8% of the time.
Solvers
Robert Bartholomew, Bob Byrne, Bob Conger, Bill Feldman,
Nick Fiechter, Steve Gallancy, Rui Guo, Clive Keating, David Promislow, Michael
Schachet, Noam Segal, Tomasz Serbinowski, John Snyder, and Al Spooner.
[1]Math. Mag. 94 (2021); pp 215-224.





