By Josh Feldman
Growing up in the ’80s in St. Louis, radio was king. Before the iPod, YouTube, or even Napster, the best way to listen to music was on the radio. Sure, MTV had launched by then, but with the city having one of the lowest cable penetration rates in the country, hardly any of my friends had the opportunity to watch the channel. And it’s not like any of our parents let us stay up late to watch Friday Night Videos! Plus, with the obscene price of records and cassettes (good luck trying to afford a compact disc player on allowance and babysitting), if one wanted to listen to music, the radio was the source. And in my pre-teenage years, the hippest, coolest station in town was 103 KHTR.
My friends and I would listen to KHTR for hours after school, talked in class about what we listened to, and would try to predict Casey Kasem’s Top 40 Countdown each weekend. Back then, it was a full-time job figuring out what to listen to. And everyone at school had no problem taking on this job free of charge. We all loved it. Even in the morning the station played music, as this was before Howard Stern and other shock-jocks hit it big.
Occasionally, the station would have concert tickets to give away. To win great seats at the big local concert venue, The Checkerdome, you had the impossible task of trying to phone into the station. While rival station Y98 would keep things simple, such as giving tickets to the 98th caller, KHTR tried something different. The station would pick a random whole number between 1 and 103, and the caller that got through would try to guess the number. If correct, the caller would win the tickets. If incorrect, the DJ would tell everyone listening if the guess was either too high or too low.
The thing was, thanks to tens of thousands of listeners and the advent of robo-callers, it was impossible to get through to the station. Hence, if one was lucky enough to get through, one can safely assume that you had one and only one guess at the number. So if you knew the lucky number was between 15 and 53, there was no incentive to pick a number like 34 which would reveal a lot of information about the true outcome of the actual number. You might as well go with your gut and guess your lucky number, no matter how long it prolongs the competition.
A couple of weeks ago, my high school friend Big S and I reminisced about these radio days and how we never did end up winning any of these contests. He then asked me (seeing as how I am supposedly the math guy) how many guesses an average contest would take. I had no clue off the top of my head, but I bet my puzzle-solving friends could help us out!
Problem: Assuming the lucky whole number is randomly distributed between 1 and 103 inclusive, all guesses are random, and that all subsequent guesses are for numbers that could still actually be the lucky number, on average how many attempts are there at this game until a winner gets selected?
This puzzle idea came from friend of the column Henk Tijms. His latest book, Basic Probability—What Every Math Student Should Know, can and should be purchased everywhere books are sold.
Note: Chi Kwok’s name accidentally got omitted from the solver’s list for last issue’s puzzle. For that, I apologize.
Solution to Previous Puzzles: More Crossnumber Problems
Crossnumber problems look like crossword puzzles, except that the answers are numbers instead of words; and the clues are the unique prime factorizations of the answers. These problems have proved to be very popular based on the large number of solvers (despite the unintended complication in Problem 3).
Although the answer grids are unique, there are many ways to solve these problems. Note also that while the prime factorizations are unique, the prime number corresponding to a given letter may not be unique because order doesn’t matter in multiplication.
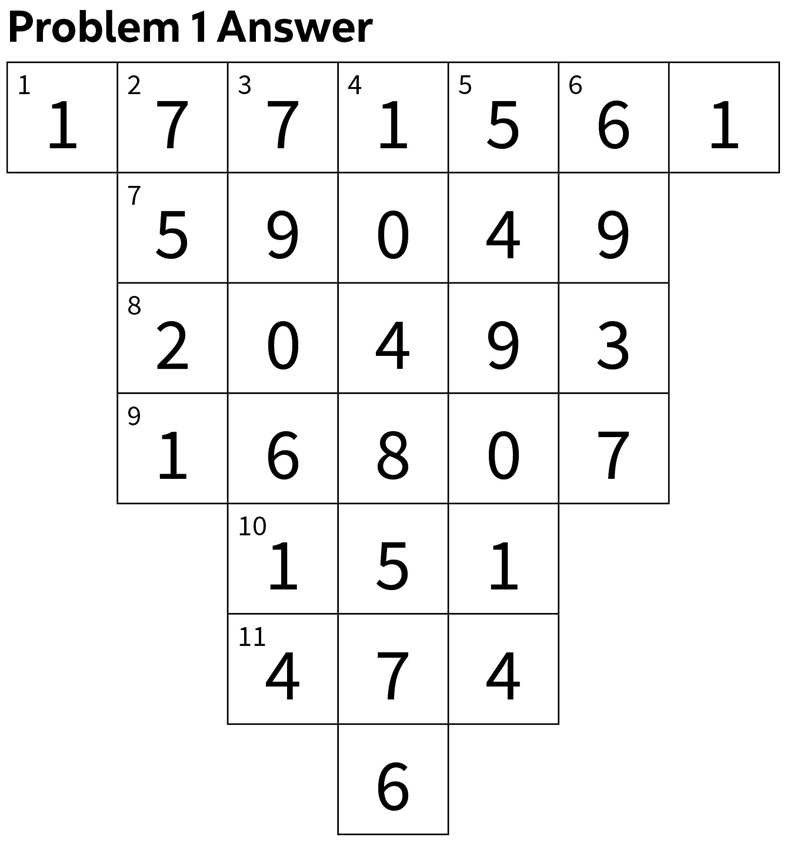
Solution: By checking powers of primes, it is not difficult to determine the values of A, B, D, and F. This allows over 70% the grid to be filled in and makes the balance of the grid easy to solve.

Solution: One approach is to note that there are only six possibilities for the six rows and columns. After factoring each of them, the answer is almost instantaneous.
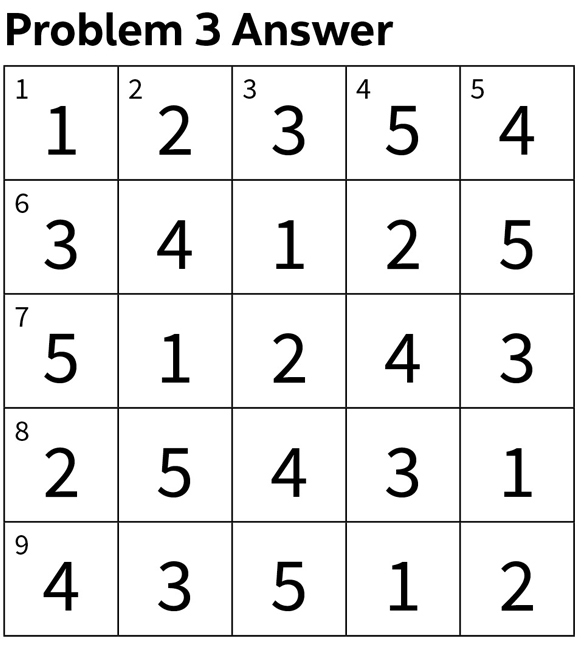
As noted by almost all solvers, the exponent in the clue for 6 Across should have been 3 rather than 2. This gaffe made for a more challenging problem.
Solution: Each row and column must be divisible by 3, so B=3. To keep 5 Down from being too big, we must have A=2. Thus, 5 Down, 1 Down, 1 Across, and 9 Across are even numbers. Precisely one row and one column must end in 5 and thus have 5 as one of their factors. The only prime that appears in exactly one of the across clues and one of the down clues is E, so E=5. Thus, 5 Down has the form: e5ooe where e is 2 or 4 and o is 1 or 3. Thus, there are only four possibilities for 5 Down. The only fit is 45312 = 28×3×59. Similarly, there are only two possibilities for 9 Across; and the only fit is 43512 = 23×3×72×37. Thus, F=7. This implies that 1 Down is divisible by 588, ends in 4, and the only fit is 13524 = 588×23. Similarly, 8 Across is divisible by 147, begins with 2, ends in 1, and the only fit is 25431 = 147×173. We can now fill in 1 Across because each digit appears once in each row and column. There are only two possibilities for 2 Down, and only one fits. The balance of the grid can now be filled in by using the method we used for 1 Across. This brings us to 6 Across = 34125 = 3×53×7×13, which shows that the correct exponent of E=5 should be 3 rather than 2.
Solvers: Dean Apps, Mike Blakeney, Samantha Casanova, Bob Conger, Andrew Dean, Deb Edwards, Samuel Ellis, Bill Feldman, Yucheng Feng, Mike Giampa, Tim Grusenmeyer, Rui Guo, Steve Itelson, David Kausch, Clive Keatinge, Alex Kozmin, Sharon Kuester, Brian Mackintosh, Jerry Miccolis, Joan Moreau, Jim Muza, Don Onnen, David Promislow, Dan N. Ropp, Anthony Salis, Leaor Schwartz, Noam Segal, Tomasz Serbinowski, Jaason Shaw, John Snyder, Al Spooner, Matt Stephenson, and Daniel Wade.





