By Stephen Meskin
For those who remember the puzzles I posed in my “Crossnumber Puzzles” (January/February 2019), the puzzles this time are to fill a 4 × 5 matrix in which each of the nine clues (four across and five down) is the same: a perfect square with the proviso that all nine perfect squares are different.
More leisurely, a Crossnumber puzzle is like a crossword puzzle in which digits are used instead of letters and the clues are mathematical. This time we are focusing on just one diagram.
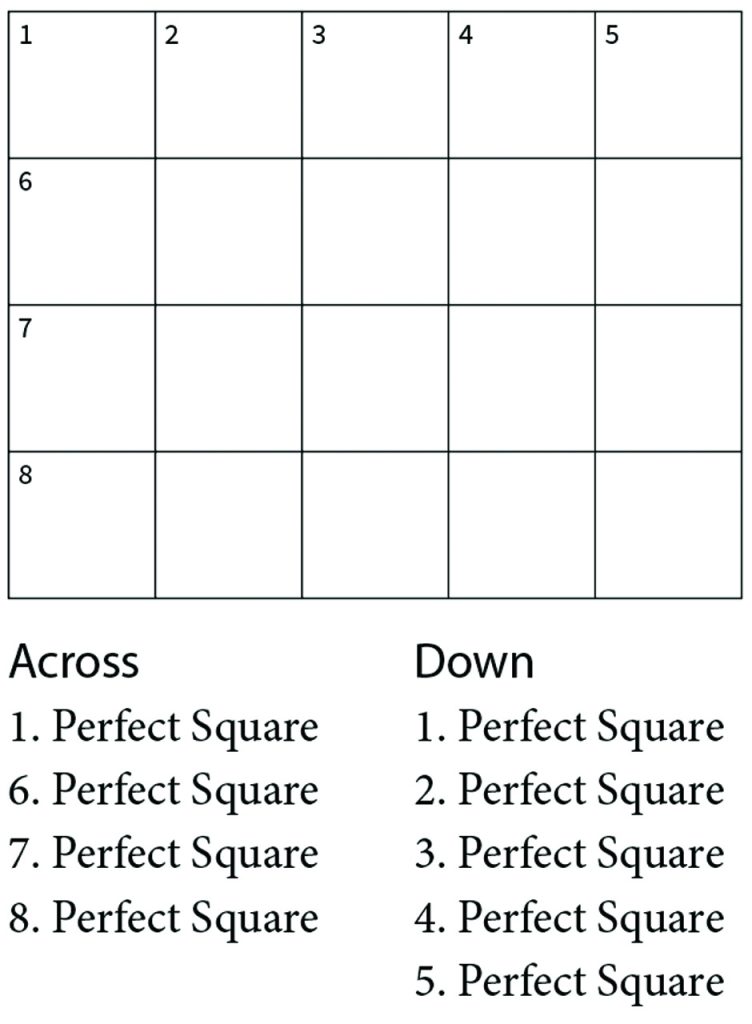
All nine entries must be different numbers, where 0016 and 00016 are the same number.
There are many solutions to the above problem, so additional restrictions will be added.
Problem One: Find a solution where 1 Across is 00000.
Problem Two: Find a solution where 1 Down is 0000.
Problem Three: Find a solution where 4 Down is 0000.
Problem Four: Find a solution where one of the other six entries is 0000 or 00000.
Problem Five: Find a solution where the 2 × 3 rectangle in the upper-left corner and the 2 × 2 square in the lower-right corner are all zeros.
Problem Six: Find a solution where 2 × 2 and 2 × 3 are interchanged in the prior problem.
Problem Seven: Find a solution that contains 14 zeros. (14 is the maximum.)
There are multiple solutions to all the above problems. The solution to the next is unique.
Problem Eight: Find a solution where none of the nine entries has leading zeroes. That is, the four across entries are true five-digit numbers and the five down entries are true four-digit numbers.[1]
Solutions may be emailed to cont.puzzles@gmail.com. In order to make the solver list, your solutions must be received by January 31, 2021.
Solutions to Prior Puzzles: The Big Wheel
1. If the first player went bust, when should the second spinner stand pat? There are a few keys to realize. One, if you spin again, your expected bonus dollars are = 0.05 × 1000 + (0.05) × (0.1) × 5000 + (0.05) × (0.05) × 50,000 = $200. Second, your estimated winnings for advancing is simply $30,000 × 0.5 = $15,000. Third, if you don’t bust (and assuming you have more than 50¢), there are five events to consider:
A. Player 3 ties you after one spin, hence a spin-off.
B. Player 3 beats you after one spin, hence you lose.
C. Player 3 loses to you after one spin and beats you with the second spin.
D. Player 3 loses to you after both spin 1 and 2.
E. Player 3 loses to you after one spin but ties you after the second.
The key is that assuming you spin 85¢, if player 3 spins between 5¢ and 80¢, it doesn’t matter what the result is, anywhere in that range there is still a 5% chance of a tie after the second spin and a 15% chance Player 3 will beat you with the final spin. Hence there aren’t nearly as many cases to consider as you might think. Given all of this, it turns out that if you spin 55¢, your expected value for standing pat is $3,975 and your expected value for spinning again is $4,337, so you will spin again. However, if you spin 60¢, your expected value for staying put is greater than that of spinning again ($4,819 vs $4,096). Hence, you should stand pat at 60¢ and above. It stinks to stand pat at 60¢ as you lose over two-thirds of the time, but it is still the right thing to do.
2. If you are the first player to spin the wheel, what values should you stand pat on? The setup is similar to part 1, but now you have to a few more cases to consider, as both the second and third player can beat or tie you. So there are now four total spins where future players can beat or tie you. But again, for each of these four spins, the probabilities remain the same (so if you spin a 90¢ for each of the four spins there is a 10% chance you will get beaten and a 5% chance of a tie). Knowing this, we can calculate everything and see that at 60¢ you want to spin again ($2,624 expected value vs. $3,025). However, things flip at 65¢, where staying leads to an EV of $3,381, vs. $2,856 of standing pat. Therefore, you want to stay at 65¢ and higher.
3. What is the probability the first spinner gets exactly $1? As we spin again 60% of the time, this is simply 0.05 + 0.6 * 0.05 = 8%. Given our work in part 2, we know how often Player 1 gets each value, so we can compute that Player 2 spins $1 8.5% of the time. Finally, using the same logic, we see that Player 3 spins exactly a dollar just over 9.7% of the time.
3. What is the probability that one player wins $50,000? Using our probabilities from part 3, we can easily see that for each group of three contestants (0.08+0.085+0.087) * 0.05 = 1.15%. As there are two groups of three who spin the wheel each show, you have a little over a 2.5% chance of this occurring in an episode.
Solvers
Rui Gio, Clive Keatinge, Zig Swistunowicz, Bob Byrne and Noam Segal





