By Josh Feldman
I never was supposed to be an actuary. Instead, once it became clear I wasn’t going to be a pro surfer, it was quietly assumed that I would follow in my dad’s footsteps and be a physicist. And for most of my early years, everything went according to plan for me to become a scientist. Of course, things have a way of changing, and the big change occurred my first semester at college.
Having passed out of Introductory Mechanics, I took 8.02 (pronounced “eight-oh-two,” otherwise known as Electricity and Magnetism) during the fall semester. Everything went fine until I took my first exam, which steamrolled me like no other exam I’d ever taken up to that point.
Still in shock over the results of that test, my dad was curious about how tough the exam really was, especially because he had taught E&M many times throughout his career. So I faxed him a copy of the exam (this was well before the advent of readily available scanners), and he tried to convince me that it wasn’t me, that the exam was crazy-hard by any standard. But by that point the damage was done.
That first exam opened my eyes to the cruel reality of college life, and after that dreadful exam-result day I told myself I would do better when the second exam comes around. So I studied and studied for the second physics test, and ended up getting a half-point above class average. By that point, I decided that if my supreme effort could barely get me above class average, maybe majoring in physics just wasn’t in the cards. So one thing led to another, and 25 or so years later here I am writing puzzles for the leading actuarial publication.
I bring this all up because after over 45 years on the job, my dad finally retired after the spring semester this year. And while I don’t remember a single thing from the physics course that I struggled in so long ago, a physics-themed puzzle sure feels in order to help cap off my father’s long run on the job. So here are a couple of puzzles that can either be solved by physics equations or by math skills that every actuary possesses. And with National Watermelon Day right around the corner—Saturday, August 3rd; mark your calendars!—here are two watermelon-themed physics puzzles for you…
To celebrate a few weeks off from the gambling scene, my friend Chef decides to throw a watermelon off the top of the largest building here in Columbia. Using satellite technology, he determined that the watermelon fell the exact same vertical distance during the first three seconds as it did during the final second before it splattered. If we assume no friction or air resistance, and that the watermelon accelerated due to gravity at a constant 10 meters per second, how far did the watermelon fall vertically before hitting the ground?
Wanting to get in on the watermelon action, my friend Big T decided to roll a watermelon off the flat roof of his condo. The roof is 10 meters off the ground, and he expertly measured that the velocity of the watermelon was precisely 5 meters a second when it left the roof. If we again assume that there is no air resistance and that the force of gravity is 10 meters per second, how far did the watermelon travel horizontally before splattering into the ground?
Solutions may be emailed to mailto:cont.puzzles@gmail.com.
In order to make the solver list, your solutions must be received by July 31, 2019.
Solution to Previous Puzzle: Four Points
The problem is to determine the number of ways of putting four distinct points in a plane so that the six line segments between the four points have two distinct lengths, where two “ways” are the same if the configurations of four points and six line segments are similar.
The answer is 6. To fully solve the problem, one not only needs to exhibit the 6 configurations but also show that there aren’t any more. Of the 32 people who submitted solutions, seven people fully solved the problem; their names are starred in the solvers list. The remaining 19 solvers exhibited 5 or 6 configurations.
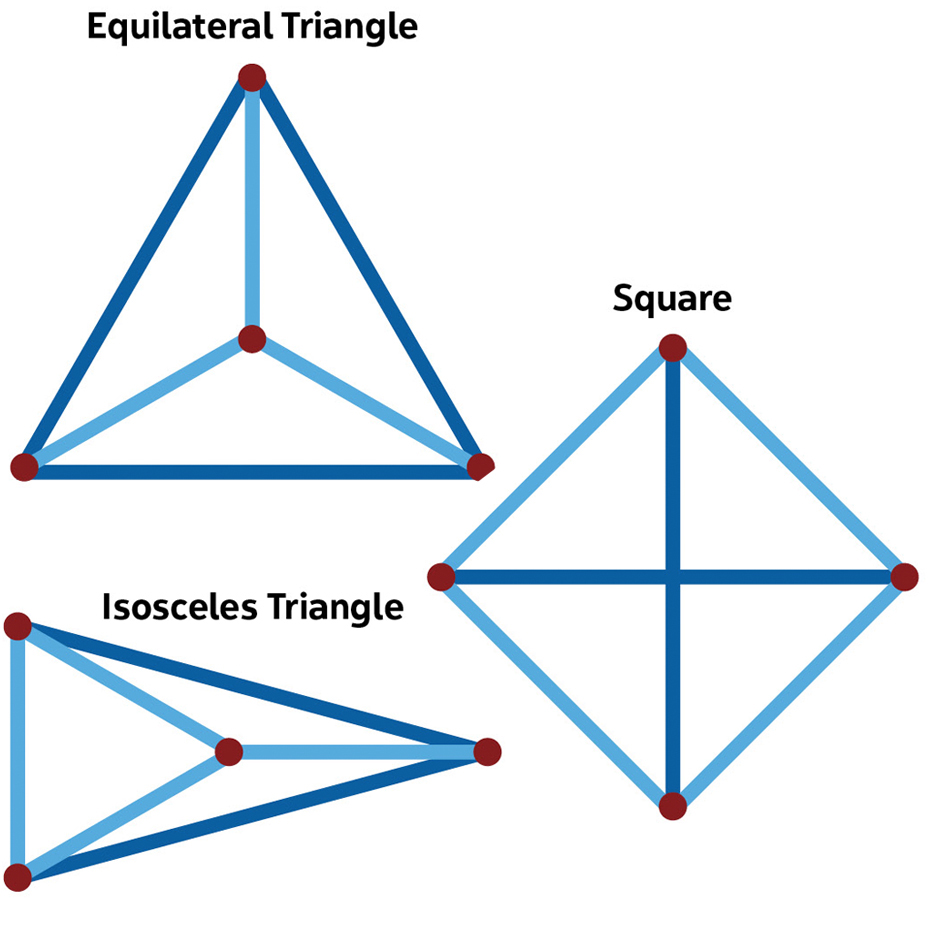
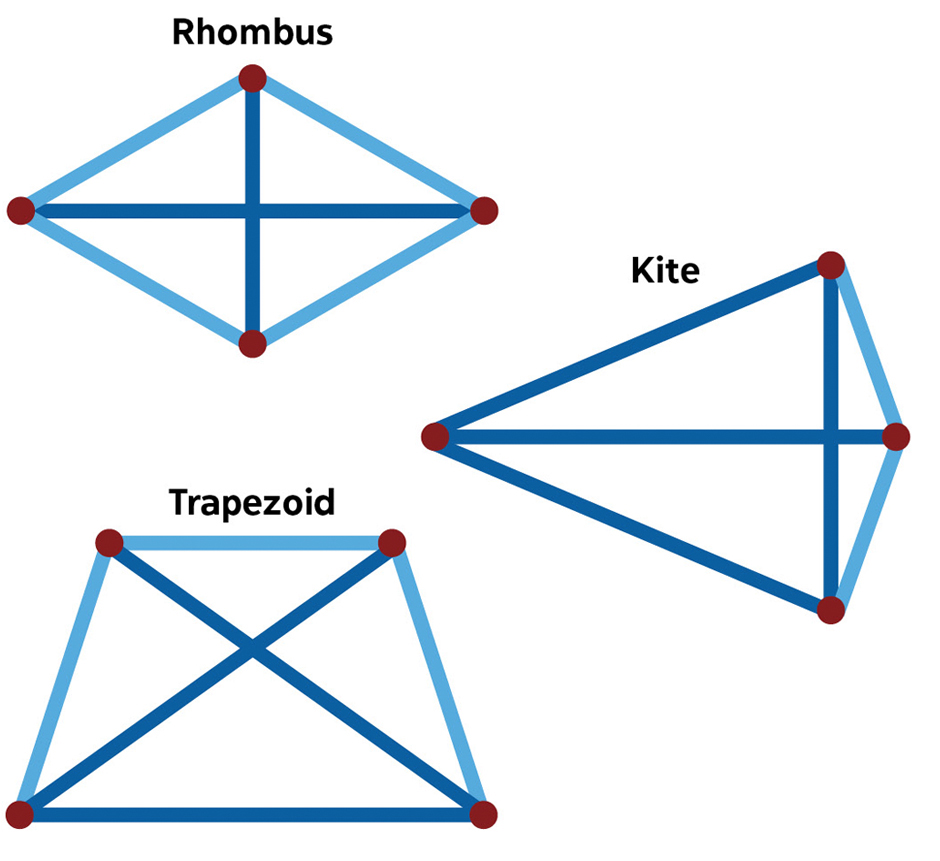
In general, the way to solve a problem like this is to create a finite list that contains all possibilities and then find all the unique items in the list. Here is a sketch of two solutions. An analytic solution is also possible.
- Start with 3 points. Show they can’t be on a line, so they form a triangle ABC. It must be isosceles and could be equilateral. We can assume AB = AC. Let D be the fourth point. If DB = DC, then D lies on the altitude from A to BC, possibly extended above A or below BC. If ABC is equilateral, show that there are four possible locations for D, each creating a distinct configuration. If ABC is not equilateral, show that it is a right triangle creating a fifth configuration. In the case that DB≠DC we get the sixth.
- Another approach is to consider the possible convex hulls of the points. (In the following, S and L indicate a short and a long segment, respectively.) The convex hull could be a triangle or a convex quadrilateral. The sides of the triangle could be LLS or LLL; show that the other (2) possibilities can’t fit a 4th point. In case the convex hull is a quadrilateral, its sides could be SSSS, SSSL, or SSLL (in that order); again, show that the others (3) can’t happen. The six configurations arise from analyzing these five cases.
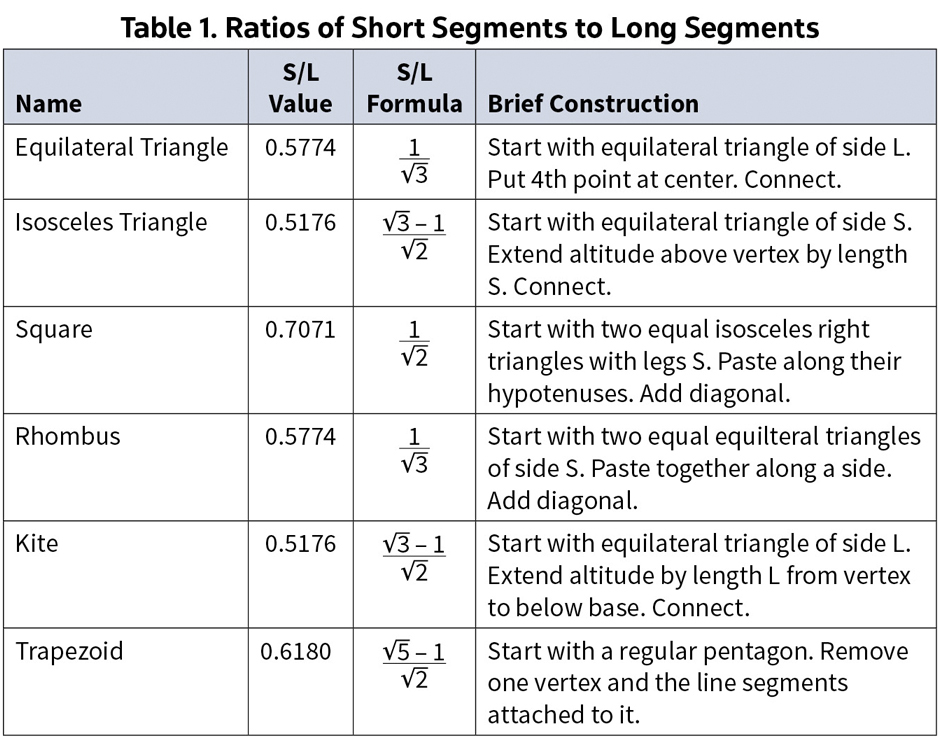
Table 1 provides some information about the six configurations, in particular, the ratios of short segments to the long segments (S/L) in each case. The limited number of configurations and the formation of the trapezoid are, in my opinion, small mathematical gems.
Solvers
Steve Altschuld, Anthony Amodeo, Robert Bartholomew, Lois Cappellano, Bob Conger*, Andrew Dean, David Engelmayer, Bernie Erickson, Bill Feldman, Zev Friedman*, Rui Guo, John Hubenschmidt, Clive Keatinge*, Alex Kozmin, Michael Murrell*, Dusty Peterson*, David Promislow, Noam Segal, Tomasz Serbinowski, Lenny Shteyman, John Snyder*, Al Spooner, Ronald Stokes, Yevgeny Venetsky, Daniel Wade*.





