By Stephen Meskin
The Federal Office of Actuaries has received an urgent call for assistance from Zack Zappa the Zoologist. He has some animals whose parts he wants to number in a specific way. He has numbered some but is having difficulty with others, and thinks an actuary could help.
He can’t put numbers on the parts themselves, only on the holders at the ends of the parts. Each part has exactly two ends, so each part has exactly two numbers. The number of a part is the absolute value of the difference of its two numbers. There are some conditions on the numbering:
- If the ends of two or more parts meet at the same point, which we will call a joint, then each of the ends meeting at that joint must have the same number. We call that the number of the joint.
- If there are N parts, the parts must be numbered 1 through N.
- The numbers on the joints must be distinct. If there are N parts and no more than N+1 joints, the numbers of the joints must be from the set {0, 1, …, N}.
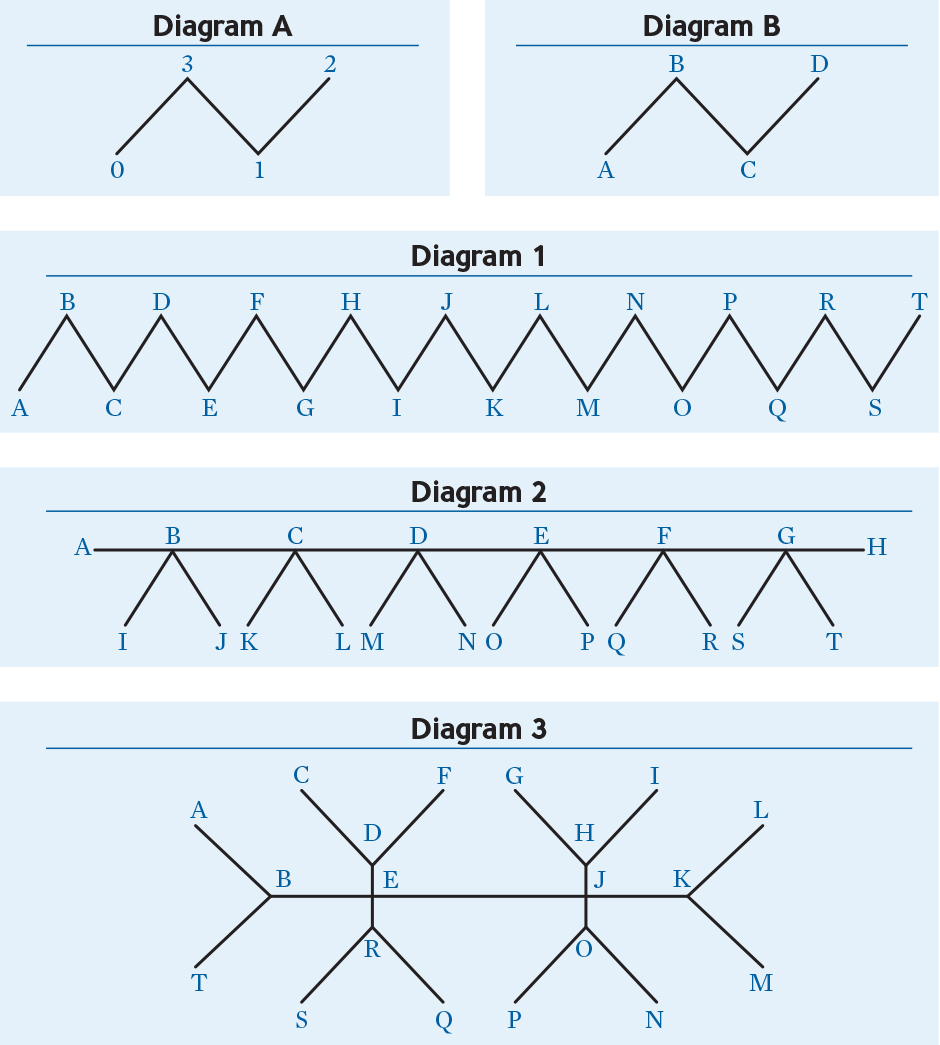
Zoologist Zach has provided an example of a numbering of a young snake (see Diagram A). As you can see, a solution consists of a numbering of the ends, which will generate a numbering of the parts that meets the three conditions.
Zoologist Zack has completed numbering all the animals with 18 parts. He has sent us diagrams of three animals with 19 parts. To make it easy to respond, he has put a letter at each of the ends. What you need to do is provide a number that corresponds to each letter. If the example in Diagram A had looked like Diagram B, then the response might have been: A-0, B-3, C-1, D-2. (Responses may not be unique.)
- The first animal is a snake.
(See Diagram 1.) - The second animal is a caterpillar with six pairs of legs. (See Diagram 2.)
- The third animal is a strange creature with six bifurcated appendages, three at one end and three at the other.
(See Diagram 3.)
| Solutions may be emailed to cont.puzzles@gmail.com.In order to make the solver list, your solutions must be received by Oct. 1, 2018. |
Solutions to Last Issue’s Puzzles—Draft Lottery Solution
A. What is the probability of the 30th-, 28th-, and 11th-place teams gaining the top three selections in the draft? Note that the sum of the number of ping-pong balls is 1 + 2 + 3 + … + 32 = 528. The probability of the 30th-place team getting the first pick is 30/528. The probability of the 28th-place place team getting the second pick in this scenario is 28/(528—30). And the probability of the 11th-place place team getting the third pick is 11/(528—30—28). Multiplying these three probabilities together gives us 9,240/123,583,680. If we continue this logic for the remaining five possibilities of order the three teams could have been selected and sum the results, the resultant probability is 0.0004317.
B. Given that the 30th-, 28th-, and 11th-place teams secured the top three lotters slots, what is the probability that each team won the lottery? We need to apply Bayes’ theorem here. There are two orders that lead to the 30th-place team winning the lottery. We saw from the first question that if 30th-place team won the lottery, 28th got the No. 2 pick, and 11th got third pick, this probability is 9,240/123,583,680. Similarly, if 30th won the lottery, 11th got the second pick, and 28th won the third pick, that probability is also 9,240/128,053,728. Summing these two results and dividing by our answer to the first problem gives us a probability of 0.34034. Using similar logic, the probability the 28th-place team got the first pick is 0.33830 and the 11th-place team nabbing the first pick is 0.32135.
C. How do these answers differ if teams can win multiple picks in the top three? Here the answer to the first problem changes to 6(30 × 28 × 11)/(528 × 527 × 526), as each of the six different orders has the same probability. For the second problem, each team has exactly a one-third chance of getting a top-three pick under these rules.
Solvers
Robert Bartholomew, Doug Bass, Bob Byrne, William
Carroll, Bob Conger, Deb Edwards, Bill Feldman, Yan Fridman, Rui Guo, Clive Keating, Chi Kwok, Eric Lemay, David Lovit, Justin Milam, Don Onnen, David Promislow, Lesley Sammarco, Mike Schachet, Noam Segal, John Snyder, Al Spooner, Daniel Wade.





