By Glenn Meyers
Since its introduction last October, the word game Wordle has gone viral. On November 1 of last year, it had 90 players. By the end of December, it had over 300,000 users. According to the New York Times, the current daily players count numbers in the millions. Included in this cohort are some of my actuarial friends.

Wordle invites the player to guess a five-letter word. After each guess, the game provides a hint that tells you whether any of your letters are in the solution, and whether they are in the correct place. You have six guesses to get the solution.
As one who likes computer programming, I thought this game was ripe for a computerized solution that would be fun to take on. But first, let’s look at the game’s history.

The game was created by a software engineer Josh Wardle, as a personal gift to his partner, Palak Shah, who loved word games. The original list of solutions had over 12,000 words. The game was a hit with family and friends, so they decided to take it public.
Most of the original 12,000 words were obscure and nearly impossible to guess. So Shah narrowed the list to about 2,500 of “the words she knew.” The remaining words were kept in a separate list as legitimate guesses.
As the game quickly grew in popularity, Wardle sold the rights to the game to the New York Times for an amount in the “low seven figures.” The Times then revised the word lists to contain only “acceptable” words. As of February 25, the solution list contained 2,309 words and the supplemental guess list had 10,638 words, making a total of 12,947 allowable guesses.
While interesting, this history is important because it reveals the fact that there is a list of solutions. One can get this list by either poking around the source code for the website, or through a Google search.

A high-level description of the program that follows is that it uses the hints to pare down the number of possible solutions (2,309 to start) as the player tries additional guesses. The goal of the program is to arrive at the solution with the fewest number of guesses.[1]
I will call this program the Robot. Here is how the Robot works.
- Pick a starting word and put it in into the NYT Wordle app, to get the colored match code. I translate: Black (or Gray)=B, Yellow=Y, Green=G.
- Enter the match code into the Robot to get a list of all possible solutions, given that match code.
- Pick one of the possible solutions, enter it into the NYT Wordle app, and get a new match code.
- If there is more than one possible solution, go back to Step 2.
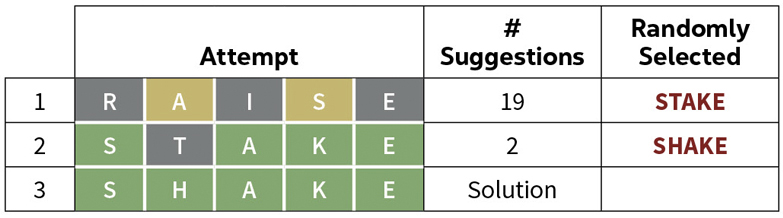
The solution to the puzzle has to appear in the list of possible solutions for each of the match codes previously entered. I have found that the number of words in such a list can run well into the hundreds. But as you enter successive match codes, the number of words that are in each of the successive lists quickly narrows to one, usually within six tries. Here is how it worked with the February 17 Wordle.
First guess – RAISE Match code – BYBYB
Suggestions – scale, shade, shake, shale, shame, shape, shave, skate, slate, snake, space, spade, stage, stake, stale, state, stave, suave and usage.
Randomly Selected Next guess – STAKE Match code – GBGGG
Suggestions – shake and snake.
Randomly Selected Next guess – SHAKE
Match code – GGGGG – Solution!
Here is a summary of this Wordle:
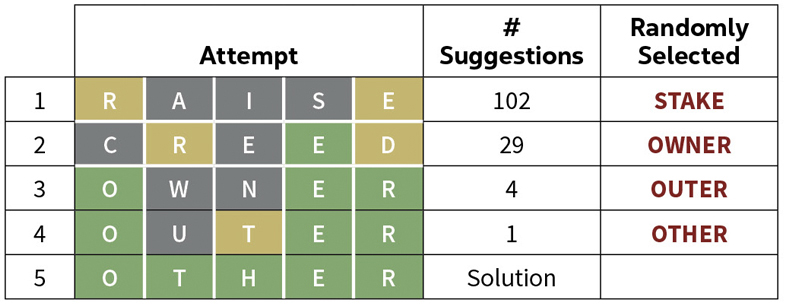
Here is another example with the February 21 Wordle.
One more example from the February 7 Wordle.
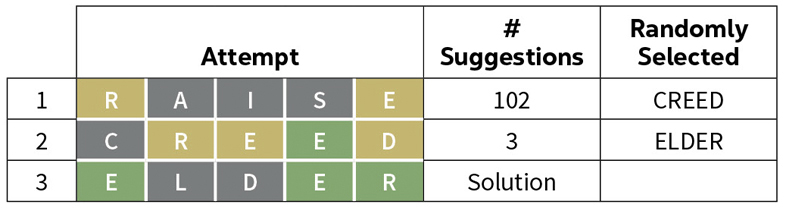
The last two examples illustrate how Wordle handles multiple occurrences of a given letter. Notice that when we match the attempt CREED with the solution OTHER the second E is given the match code G meaning that the second E is in the correct position. Since there are no other Es in the solution, the first E is given the match code B.
When we match the attempt CREED with the solution ELDER as in the previous example, the second E is given the match code G, but since there is another E in the solution, the first E is given the match code Y.

Summarizing, I have demonstrated a way to solve a given Wordle puzzle by taking a (random?) sequence of guesses and eventually arrive at a solution. Let’s now address how to choose our sequence of guesses to minimize the number of attempts.[2] I will begin with the problem of choosing the initial guess.
When we take a guess of the solution, we get a accompanying match code. We regard the pair (guess, match code) as “information.” The question to ask is then: What guess, along with the accompanying match code, provides us with the most information. To answer this, we first need to define what we mean by “information.” First let’s try to formulate an intuitive idea of what information is.

We say that a guess has:
- One bit of information if it reduces the number of possible solutions by a factor of 1/2.
- Two bits of information if it reduces the number of possible solutions by a factor of 1/4.
- I bits of information if it reduces the number of possible solutions by a factor of (1/2)I. Note that I need not be an integer.
Now let:
- N0 (initially 2,309) be the number of possible solutions.
- N1 be the number of possible solutions after entering the match code for the latest guess.
Then let P = N0 / N1. Then the amount of information, I, is defined by the equation P = (1/2)I = 2-I. Solving this equation for I yields I = – log2(P).
In the first example above the first guess reduced the number of possible solutions from 2,309 to 19. We then have I = – log2(19/2309) = 6.925). In the next two examples the first guess reduced the number of solutions to 102. We have I = – log2(102/2309) = 4.501.
When selecting a starting word, one wants to select the one that gives us the most “information” as defined above. But the information statistic depends on the solution as well as the starting word. When we don’t know the solution we proceed by calculating the information statistic for each of the 2,309 possible solutions, and taking the average. This calculation is fairly time consuming, but it only needs to be done once for a given starting word.
An internet search yields several suggestions for initial guesses, and I selected a set of 20 and calculated the average information over all 2,309 possible solutions. The results are in the following table.
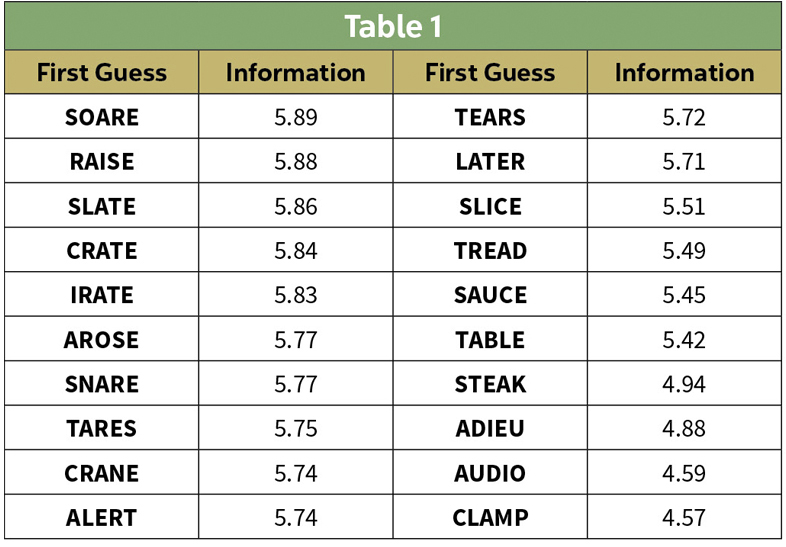
Now that we have some information statistics, let’s see if they help us solve Wordle puzzles any faster. To test this I calculated the number of attempts it took to find the solution all 2,309 possible solution with my current favorite, RAISE, with an early favorite ADIEU. I plotted the results in the Figure 1.
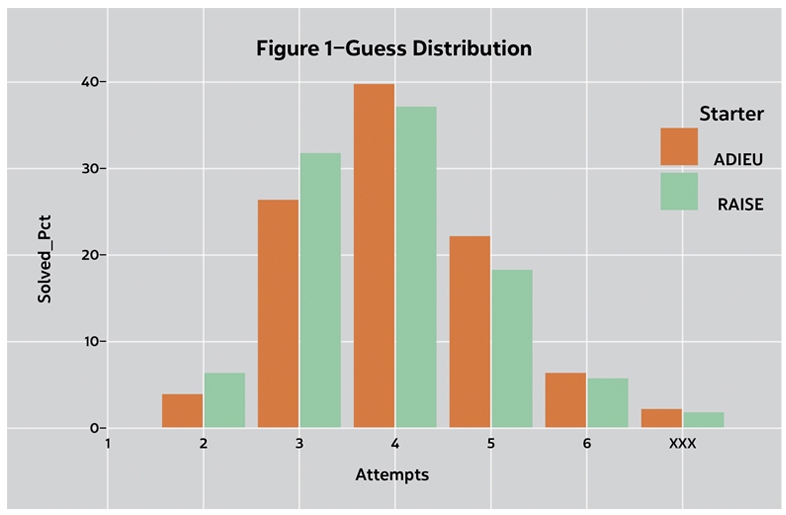
Here we can see that a first guess with more information tends to yield a faster solution.
I should point out that the above bar chart was produced using an early version of the Robot. After using the selected initial guess, the Robot selected the subsequent guesses at random. So I asked—can we improve on this?
My first thought was to do what I did for the first round—calculate the expected information for each of the remaining possibilities. It is a time-consuming calculation for the first round, but we need perform it only once. The information obtained from the subsequent rounds will depend on the results from the earlier rounds, so I needed to calculate the information on the fly. I originally thought this might work as the list of possible solutions grew shorter as the rounds progressed.

But the number of possibilities in the second round was often in the hundreds and the calculation took several minutes. So I decided to take a random sample of the remaining possible solutions and use the solution in the sample that yielded the maximum information. After some trial and error I settled on a maximum sample size of 25. The computing time was barely noticeable, and the results were barely distinguishable from larger samples.
Figure 2 shows that selecting the next guess based on the maximum information of (a sample of) the possible next guesses tends to decrease the number of guesses needed to get the solution. The initial guess was RAISE for both plots. The blue bars in Figure 2 are identical to the blue bars in Figure 1.
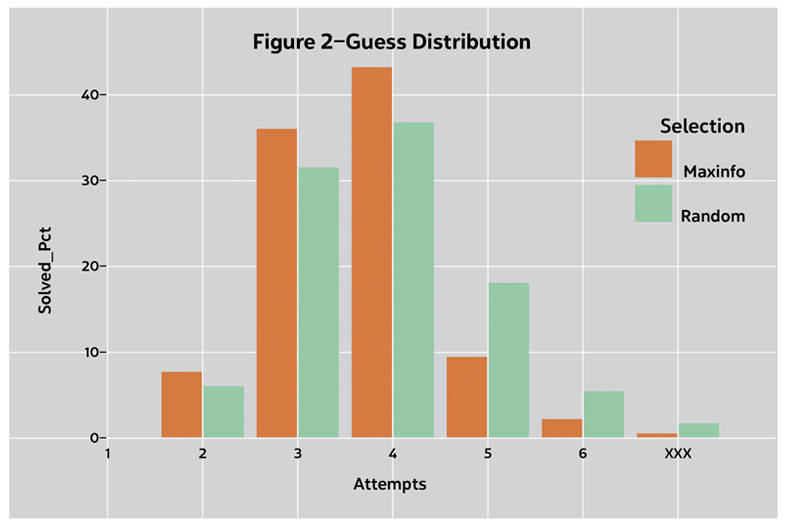
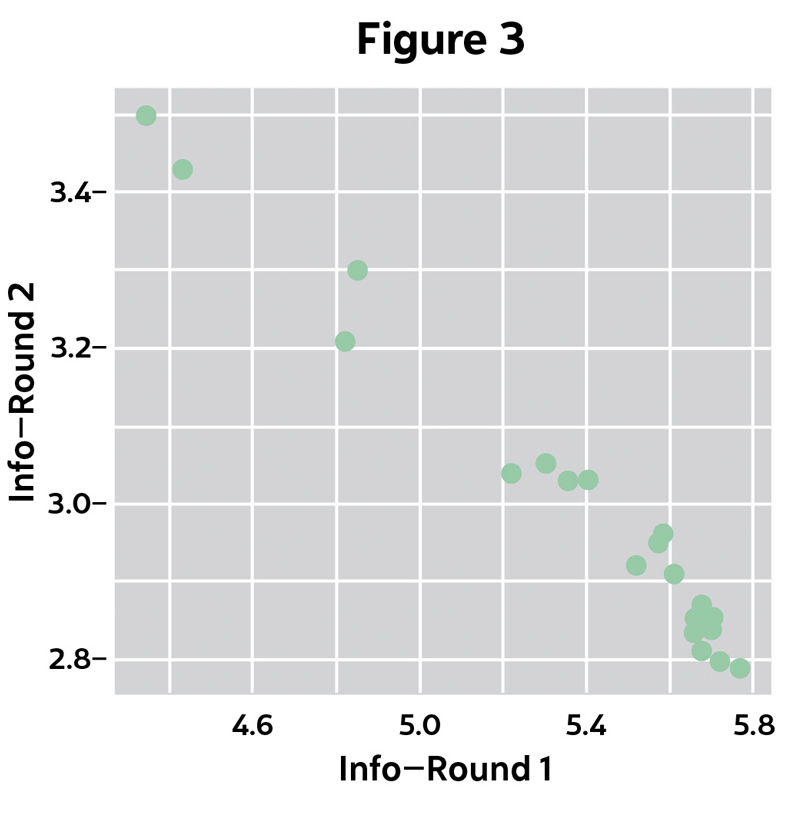
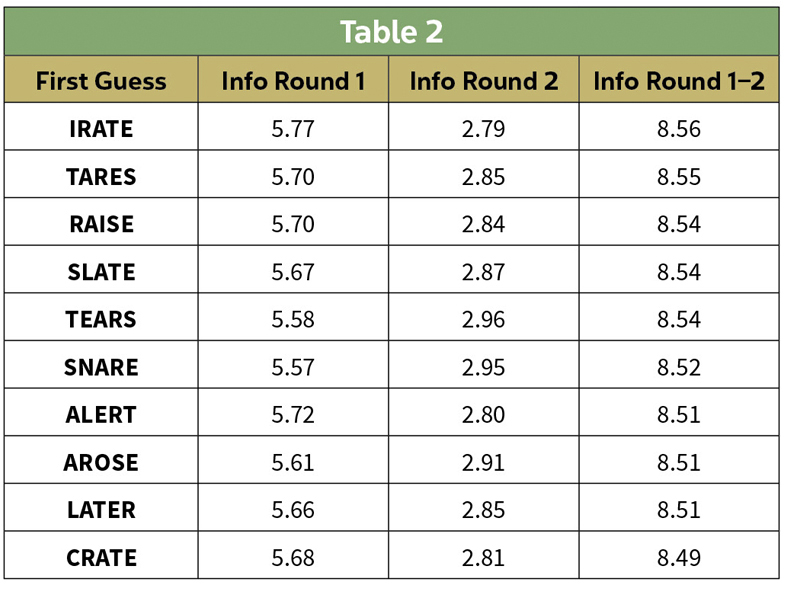
Next I asked the question: If I make my guesses with the MaxInfo strategy, should I change my initial guess? To answer this, I solved the puzzle for a sample of 250 possible solutions while keeping track of the information added in Rounds 1 and 2, for each of the starting words in Table 1 above.[3]

Notice in Figure 3 that the information gained in Round 2 is inversely related to the information gained in Round 1. Then in Figure 4 we see:
- The total information gains from both rounds span a much smaller range than the information gained from the first round alone.
- There is little difference between the best starting words using the MaxInfo strategy.
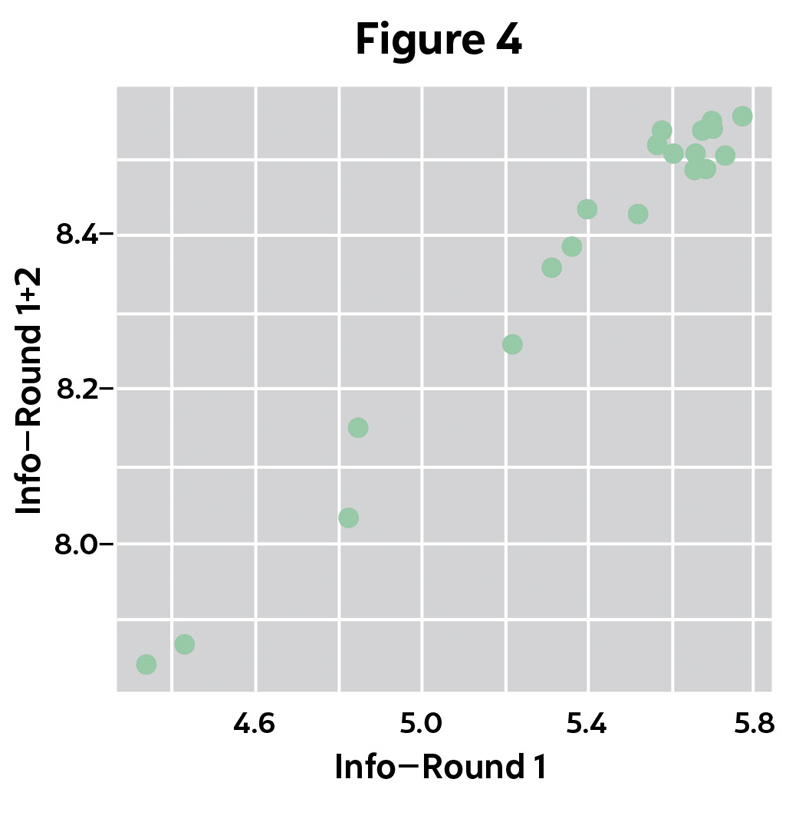
The bunching of total information gains at the top led me to randomly select first guess from Table 2 below in the current version of the Robot.

Solving short word puzzles has been part of my daily routine for decades. I usually do Wordle manually when I first open my online newspaper on my tablet. So far anyway, I run the Robot later in the day when I get to my computer. I like running the Robot because I can look at the alternative guesses. When doing Wordle manually, I feel lucky if I can think of more than three alternative guesses in any given round.
I submitted this article to Contingencies because I think actuaries may find information theory useful in some of their professional work. So have at it!
GLENN MEYERS, MAAA, FCAS, is an avid puzzler.
[1] One may argue that I am cheating by looking at this list. If so, I freely admit it. But the ideas in this article will apply to any list. What is important is that the guesses depend only on the hints suppled by the NYT app and a mathematical formula.
[2] This article was inspired by two posts on Wordle by the YouTuber Grant Sanderson on his website 3blue1brown.com.
[3] With the MaxInfo strategy, the Robot runs a single Wordle puzzle quickly. But running 2,309 puzzles takes an inordinate amount of time. So I sampled, and I attribute the differences between Table 1 and Table 2 to sampling error.




