By Stephen Meskin
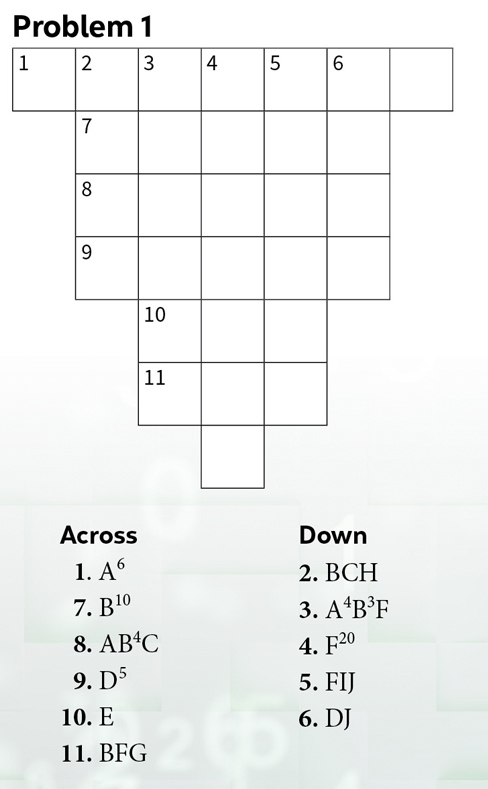
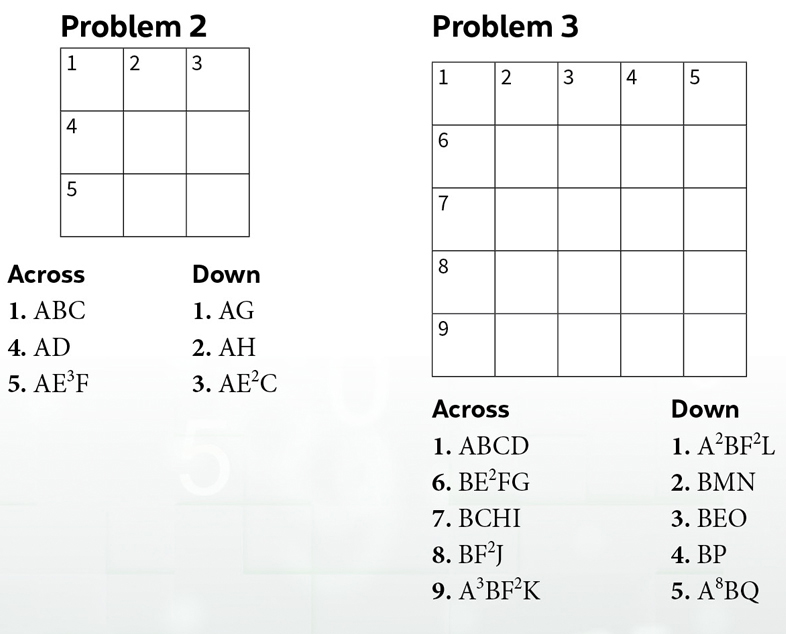
Back by popular demand, we have a few crossnumber problems. These types of problems were introduced in this column in January/February 2019. Those presented here are basically the same as before, with little twists. The problems look like crossword puzzles, except that the answers are numbers instead of words, with digits in place of letters. The clues are the unique prime factorizations of the answers. The prime factorizations are sequences of capital letters. Each prime number is represented by a single capital letter; the representation is unique within a given problem. It is helpful to know that the answers have no leading zeroes.
The little twist in Problem 1 is its shape. For Problems 2 and 3, we go back to nxn squares but add the requirement that every row and every column of the nxn square contains every digit from 1 to n inclusively (thus no zeroes at all). You may think that this information makes the problem easier. You are right, but on the other hand it allows the creator of the problem to pose a harder problem. Indeed, if you get frustrated with Problem 3, you’ll find a hint that might turn you around.
Solutions may be emailed to cont.puzzles@gmail.com.
In order to make the solver list, your solutions must be received by June 1, 2023.
Solution to Previous Puzzles: Death by Quarters
1. What is the probability Doc and Hoss are tied after 50 races? This is simply a binomial distribution in which there are 50 events with a probability of 0.5 for each of them, where each ends up with 25. Or ( )( ) = 11.2%.
2. What is the probability that one runner would lead the competition after each of the 50 races? This is a type of Bertrand’s Ballot problem. Bertrand’s Ballot Theorem states that in an election, if the winning candidate receives p votes and the losing candidate receives q votes, then the probability that the winning candidate will be ahead after every vote is read is simply .
In our problem, it is possible to win the competition by scores of 26 to 24, 28 to 22, 30 to 20 … 48 to 2, and 50 to 0. We can use the binomial theorem combined with Bertrand’s Ballot Theorem to then get us the answer. Doing this leads to 5.61%—but we need to multiply this by 2, as both candidates have the possibility to have the lead throughout the event. 5.61%*2 = 11.2%, which surprisingly is the same answer as question 1!
3. What is the probability of a runner never being in the lead throughout the competition but the competition ends up tied? After two races, either one runner has won both races or the runners split the first two heats. But in either case, we still have a chance to hit our preferred outcome., For race three, either a runner will take a 3-0 lead or it will be a 2-1 lead., If the racers are tied after 2, then there is a 50% chance the winner of heat 1 will also win heat three, but if the winner of heat two also wins heat three this will not be a case where both runners had the lead at some point. We can keep building this out in Excel using the same logic and see what the probability is that the runners end up tied with one runner having never led. After building our logic tree out for 50 races, it turns out that this probability is 0.9%.
Solvers: Bob Byrne, Samantha Casanova, Bob Conger, Samuel Ellis, Rui Gio, David Kausch, Clive Keating, David Promislow, Jason Shaw, Al Spooner, and Daniel Wade.





