By Paul Meixler
Models are ubiquitous in actuarial work. The following is a synopsis of the languages of models—in particular, the complex metalanguages and the structured rule-based object languages of models, along with mappings between them, are described.
Actuaries maintain a high standard of professional conduct relevant to their practice domain through literacy in the Code of Professional Conduct and the actuarial standards of practice (ASOPs). The Code and the ASOPs provide guidance in the English language that reflect the professional and ethical standards of actuarial practices in the United States. English is used in the Code and ASOPs as the metalanguage. ASOP No. 1, Introductory Standard of Practice, provides, for example, foundational metalanguage definitions used by other ASOPs, including definitions of the words must and should. Awareness of the difference in these words has an important connection to professionalism.
ASOP No. 56, Modeling, became effective October 1, 2020, and “provides guidance to actuaries when performing actuarial services with respect to designing, developing, selecting, modifying, using, reviewing, or evaluating models.” It is written with defined terms and principles in a metalanguage. An implemented model is written in an object language, which is generally a computer language. Excel, for example, is an object language that provides the function Present Value (PV) that models the current value of an expected future stream of cash flow from the data inputs: rate, period, and payments. Excel’s PV function is part of the object language and maps to the definition of the term present value in a metalanguage.
Analogous to an actuary learning the ASOPs, when young children start school, they may encounter unknown standards of conduct, and they gradually learn to adjust by learning new skills. The children learn, for example, to raise their hand to request a turn to speak. Their educational setting strives to assist them in learning linguistic and analytic skills along with existence skills. During a beginning English reading class, for example, the children are required to communicate in English about the linguistic activities with words such as page, line, space, and comma. The language used for this communication is the metalanguage. The children’s awareness of the metalanguage of literacy is connected to their subsequent performance in reading and writing.[1]
A similar linguistic situation arises when students learn a second language. Their mother tongue, along with grammatical terms and rules, forms the metalanguage. The second language is the object language. English speakers may use a French grammar book written in English to learn French. Polyglots—persons who read, speak, or understand many languages—have awareness of the metalanguage for many natural languages. They easily compare the metalanguages of the individual natural languages. The different natural languages use different combinations of phonemes or letters for a word; a word of type noun, for example, is a name for the same kinds of things. The challenge for polyglots is to map related names between the ontologies underlying the different natural languages.
Ontology is the study of the collections of individual things that exist or may exist in some domain. It is the study of existence, of all kinds of things—abstract and concrete—that make up a domain. Two sources of determining ontological collections are observation and reasoning. Observations provide knowledge of the physical world and reasoning makes sense of the observations using language. The choice of the ontological collections is the first step in designing a scientific model. The selection of the collections determines everything that may be determined from the model.[2]
When domain experts interact among themselves and refer to different choices of the ontological collections, there is ontological uncertainty. It not only involves referring to different collections but also referring to differences of what and how the collections interact with each other. In contrast to ontological uncertainty, semantic uncertainty is a result of the differences between the meanings given by different domain experts to the words used in their metalanguage, or vague and ambiguous definitions used by the domain expert. A domain expert uses a natural language as the metalanguage for the purposes of communicating about their domain.
A detailed discussion of metalanguage and object language is provided in Introduction to Symbolic Logic and its Applications by Rudolf Carnap. He states, “A natural language is given by historical fact, hence its description is based on empirical investigation. In contrast, an artificial language is given by the construction of rules for it. The rules of an object language, as well as theorems based on these rules, are formulated in the metalanguage.”[3]
The goal of professional standards is to reduce the ontological and semantic uncertainty in the communication of information. The ASOPs’ purpose is to address these difficulties. The ontology and semantics of the ASOPs standardizes terminology used to classify and find information. As an example, let’s look at a couple of definitions from Actuarial Standard of Practice No. 56, Modeling.
- Model—A simplified representation of relationships among real world variables, entities, or events using statistical, financial, economic, mathematical, non-quantitative, or scientific concepts and equations. A model consists of three components: an information input component, which delivers data and assumptions to the model; a processing component, which transforms input into output; and a results component, which translates the output into useful business information.
- Data—Facts or information that are either direct input to a model or inform the selection of input. Data may be collected from sources such as records, experience, experiments, surveys, observations, benefit plan or policy provisions, or output from other models.
From the Excel example mentioned before, a cell with a formula in Excel meets the definition of a model. The object language formula “=PV(0.05, 5, 1)” in cell A1 has a input component “0.05, 5, 1” (rate, period, and payments) including the assumption (discount rate of 5%) and data (periodic payments of 1 for 5 years). It also has a processing component “PV()”, and a results component show as “($4.33)“. The formula “=A1*10” in cell A2 has the result component “($43.29)”. The assumptions and data of the model in cell A2 uses the output from the model in cell A1. (See Figure 1.)

The metalanguage provides the translation of the information to and from the object language. The translation of output of the Excel PV() function is “Returns a present value of an investment: the total amount of a series of future payments is worth now.” The formulas are written in a structured rule-based object language, Excel, modeling the actuarial concept of “present value” in a complex metalanguage using English.
As illustrated by this Excel example and what many computer programmers say, the complexity of designing a computer program (in our case models) is not manipulating a known object language, it is the understanding and translating the metalanguage into the object language, translating the ontology and semantics of a specific domain. Understanding “the total amount of a series of future payments is worth now” is simple for a trained actuary; however, it is quite complex for a person without financial literacy.
From the computation viewpoint, “The purpose of a program describes a computational process that consumes some information and produces new information. For a program to process information, it must turn it into some form of data in the programming language, then it processes the data; and once it is finished, it turns the resulting data into information again.”[4] Translating information into data is called “to represent.” Translating data into information is called “to interpret.”
Using the Excel example, information is at the level of the metalanguage and data is at the level of the object language. The data of the object language, Excel’s PV() function, is “0.05, 5, 1”, which represents information related to discount rate assumption, period, and payments. Based on this data, the information provides an answer or is interpreted as “what the total amount of a series of future payments is worth now” or “has the value now”. In this example, the information that the discount rate is 5% and periodic payments of 1 for 5 years is used to produce more information—the present value of this information has a value now of ($4.33).
Another way to represent data is with a relational database schema. A relational database has tables each consisting of a collection of columns and a collection of rows. Each database table is like an Excel worksheet; however, each database table also has a primary key generally in the leftmost column and the cells in the other columns have foreign keys. The foreign key columns link one table to another. In a completely normalized relational database, all the tables are mathematical sets; i.e., each element of the ontological collection is unique. Using mathematical graphs, the conceptual layout of data represents the schema.[5] The graphs can visually reflect complex layers of data relationships.
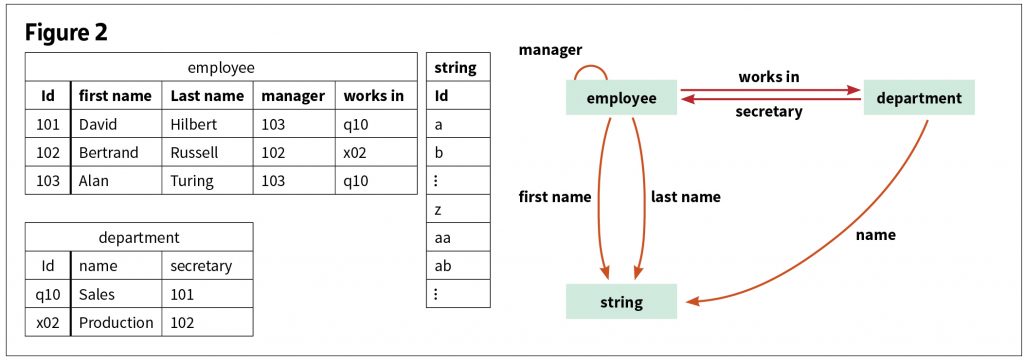
Figure 2 is an example of a database instance and schema.[6] It includes two business rules: (1) every employee works in the same department as his or her manager, and (2) every department’s secretary works in that department. The instance is on the left and the corresponding schema is on the right.
Similarly, the object language consists of complex systems of sublanguages with a stratified design. The “complex systems should be structured as a sequence of levels that are described using a sequence of languages. Each level is constructed by combining parts that are regarded as primitive at that level, and the parts that constructed at each level are used as primitives at the next level. The language used at each level has primitives, means of combinations, and means of abstraction appropriate to that level of detail.”[7]
The task of the programmer (in our case the modeler) is to go back-in-forth translating between the metalanguage and the object language, and to eliminate the ontological and semantic uncertainty. In other words, the task is to use a precise and testable translation of the model languages at all the data and language levels. A mathematically rigorous approach is available to address the ontological and semantic uncertainty. Ontological collections in the metalanguage represent data by mathematical sets—a set semantics. Applying this rigor opens a warehouse of mathematical tools available through Applied Category Theory. Relatively recent developments regarding this approach are introduced below.
In 1945, in General Theory of Natural Equivalences, Samuel Eilenberg and Saunders MacLane introduced the concepts of category, functor, and natural transformation. In the past 70 years, category theory has flourished. “Category theory has found applications in a wide range of disciplines outside of pure mathematics—even beyond the closely related fields of computer science and quantum physics. These disciplines include chemistry, neuroscience, systems biology, natural language processing, causality, network theory, dynamical systems, and database theory to name a few. And what do they all have in common? … In other words, the techniques, tools, and ideas of category theory are being used to identify recurring themes across these various disciplines with the purpose of making them a little more formal.”[8]
Using metalanguage, a category is defined as a collection of individual things that have related characteristics. The definition of a category is separated into two items and two rules. The items are (1) collection of individual things and (2) a type of relationship between pairs of individual things. The rules are (1) every individual thing is related to itself by simply being itself, and (2) if one individual thing is related to another and the second is related to a third, then the first is related to the third.[9] In the object language, category theory, the individual things are called objects and the relationships are called morphisms.
Let’s look again at the definitions of model and data from ASOP No. 56, this time with bolding judiciously applied:
- Model—A simplified representation of relationships among real world variables, entities, or events using statistical, financial, economic, mathematical, non-quantitative, or scientific concepts and equations. A model consists of three components: an information input component, which delivers data and assumptions to the model; a processing component, which transforms input into output; and a results component, which translates the output into useful business information.
- Data—Facts or information that are either direct input to a model or inform the selection of input. Data may be collected from sources such as records, experience, experiments, surveys, observations, benefit plan or policy provisions, or output from other models.
These definitions remind me of Rule 2 of a category. In the definition of Model bolded above, the processing component that transforms input into output looks like a morphism. In the definition of Data bolded above, the input may be output from other models looks like the output from the first morphism is the input for the second morphism. From the Excel example, the output from the formula “=PV(0.05, 5, 1)” in cell A1 is used as the input for the formula “=A1*10” in cell A2. In other words, each cell looks like a morphism and the morphisms compose. The input components in the ASOP No. 56 definition of model would then be the representation of information in the metalanguage with data (and assumption) in the object language. The result components would be the interpretation of data (and assumption) in the object language with information in the metalanguage.
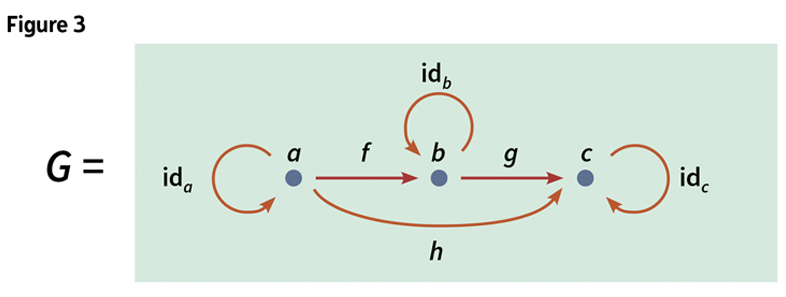
A category can be visually thought of as a reflexive directed graph with vertices and arrows. In a graph, every arrow points from a vertex to a vertex, just as in a category, every morphism points from an object to an object. There may be many arrows between two vertices a and b, like many morphisms may be between objects a and b in a category—or there may be none. There is at least one arrow from a to itself like the identity morphism in a category that is required for each object. In the graph representation of a category, the composed morphisms are generally not shown on the graph to avoid the clutter of too many arrows. Categories are distinguished from graphs by the ability to declare an equivalence relation on the set of paths. (See Figure 3.)
In Category Theory for the Sciences, David Spivak introduces category theory with examples from different disciplines. One discipline of interest is database theory using a set semantics. He develops a formal metalanguage using natural language and category theory to define data definitions. The data definitions use “ontology logs” or “olog” for short. Ologs are designed to record the results of a study of existence, of all kinds of things—abstract and concrete—that make up the world in a particular domain. An olog represents a worldview, discrepancies between worldviews reflect different realities, and different ologs would be created for different worldviews. The rules to create an olog are enforced to ensure that an olog is structurally sound, rather than it “correctly reflects reality.”
In creating the ologs, the ologs are the object language used to define the ontological collections. English as used by the domain expert, for our purposes, is the metalanguage. In creating the database theory schema, the ologs then become the metalanguage and category theory is object language. In creating the actual database instance, the category theory used for the schema is the metalanguage and the data in the instance is the object language. As with database theory, the data used in a model is a complex system of sublanguages with a stratified design. Ologs enable the modeler to think with an ontological and semantic viewpoint about the phenomena in different ways—ontological primitives, means of combinations, and means of abstraction that can be well suited to a particular phenomenon.
“A basic olog is a category in which the objects and arrows (morphisms) have been labeled by English-language phrases that indicate their intended meaning. The objects represent types of things, the arrows represent functional relationships (also known as aspects, attributes, or observables), and the commutative diagrams represent facts.”[10] The objects are types, collections of individual things, placed in a text box and labeled with a singular indefinite noun phrase.
The morphisms of this category are aspects, ways of viewing or measuring it, shown with arrows. It is drawn as a labeled arrow from an object to a “set of result values.” For example, an employee can be regarded as a person. That is, “being a person” is an aspect of an employee.
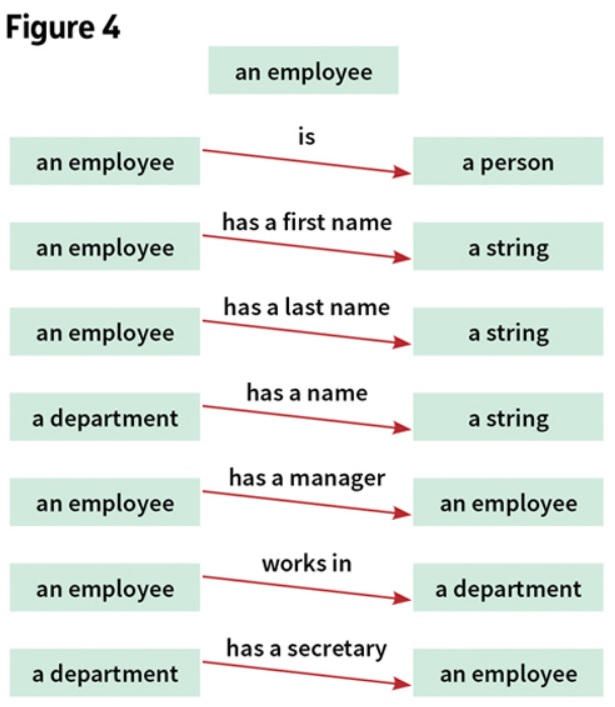
The aspects from the database instance and schema above are shown in Figure 4.
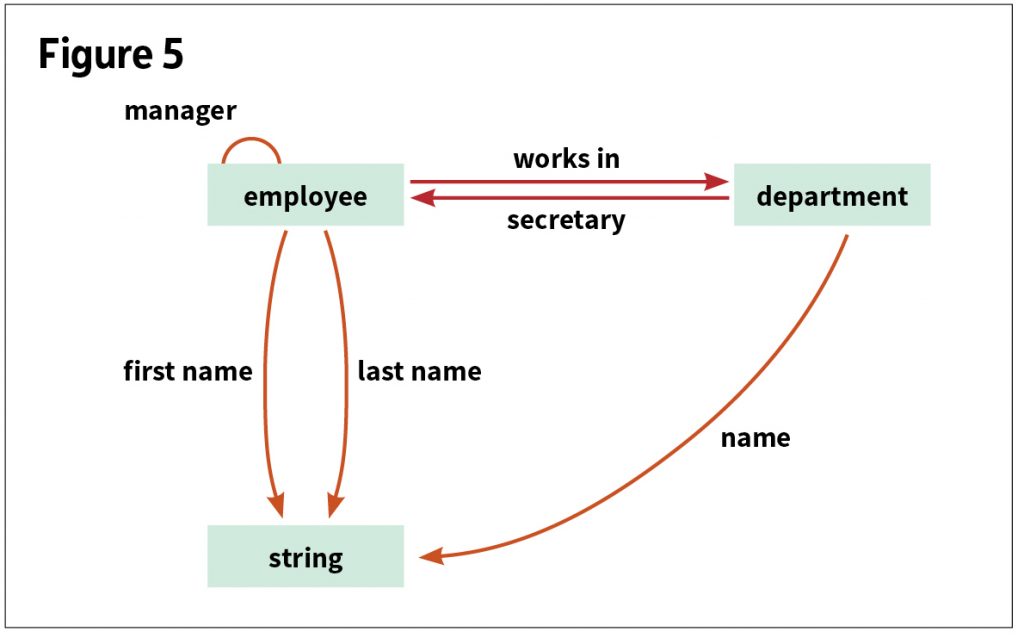
The arrows above are then composed to form the schema shown in Figure 5.
The schema is loaded with mathematical sets of data to form an instance. In a completely normalized relational database, all the tables are mathematical sets; i.e., each element of the ontological collection is unique. For this schema, data from Figure 6 are used in the database tables in the instances above.

Each type is assigned a mathematical set of instances. In other words, the elements of the set have unique elements. In the FirstNameString set, the name “Bertrand” only occurs once without any duplicates.
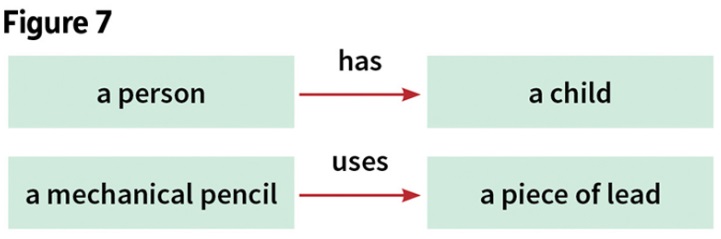
For ologs, the types in a text box are ontological collections of individual things. They are mathematical sets. What makes an aspect or arrow “valid” is that it must be a mathematical function. A mathematical function is a mapping that sends each element of the domain to an element of the co-domain; that is, for every element x of the domain, there is exactly one map emanating from x, but for an element y of the co-domain, there may be several or no maps pointing to it. The two arrows shown below in Figure 7 are not mathematical functions. The first arrow is invalid because a person may have no or many children. The second arrow is invalid because a mechanical pencil may have many pieces of lead that it uses.
An aspect is read as an English phrase. Each aspect is read by first reading the domain text box, then the arrow, and finally the co-domain text box. Paths of aspects are read by inserting the word “which” after each intermediate text box. For example, the following path is read “an employee is a person, which has as a birthday a date which includes a year. (See Figure 8.)

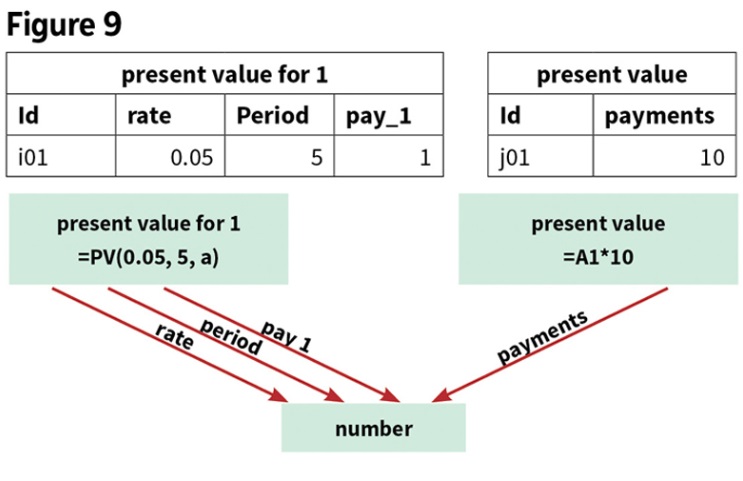
Let’s illustrate using the original example, where the object language formula “=PV(0.05, 5, 1)” in cell A1 has a input component “0.05, 5, 1” (rate, period, and payments) including the assumption (discount rate of 5%) and data (periodic payments of 1 for 5 years), and the formula “=A1*10” in cell A2. Our original metalanguage was “Returns a present value of an investment: the total amount of a series of future payments is worth now.” Another version of this metalanguage: The function Present Value (PV) models the current value of an expected future stream of cash flow from the data inputs: rate, period, and payments. The model for the data in terms of an olog is shown in Figure 9.
A fact in terms of an olog is shown in Figure 10.
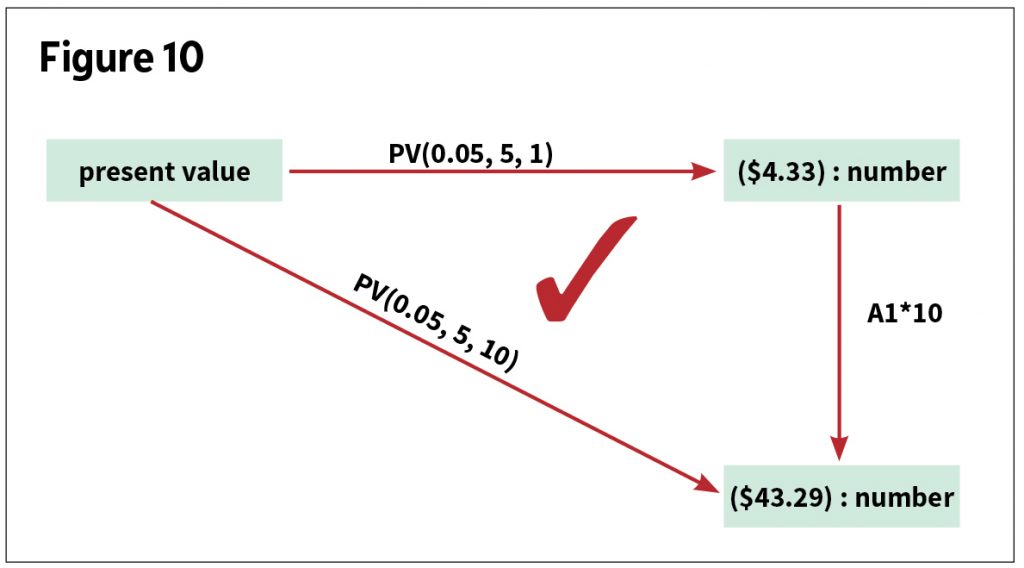
This olog illustrates the fact that the present value of 1 times 10 produces the same result at the present value of 10. In a category (an olog in this example), there may be an equivalence relation on the set of paths. Paths of morphisms in a category that result in the same result are said to be commutative. In ologs, they are facts.
Another consideration of a model not discussed in this article is the logic used in the object language. Even with standard terminology, computational side effects of the model may cause some results to be different in different computer systems. Even with standard terminology and no side effects, results may be different due to different variations of logic. Classical mathematics, for example, is done in the topos of Set (Set Semantics) with its internal logic the “ordinary” logic.[11] It includes the principle of excluded middle and the full axiom of choice, and methods such as proof by contradiction. In contrast, constructive mathematics is done without these in different topos. Ologs use a Set semantics with “ordinary” logic.
As a concluding remark, this article was tailored for an audience of actuaries in the American Academy of Actuaries who may find ologs pleasing to their visual cortices. The application of these concepts can be adopted to other domains and could be tailored for audiences of other scientific organizations. Scientists have a pressing need to adopt metalanguages “that organize their experiments, their data, their results, and their conclusions into a framework such that this work is reusable, transferable, and comparable with the work of other scientists.”[12] Ologs also provide the intermediate language—first as an object language from which the scientists can make concepts in their metalanguage precise, and then as the metalanguage for translation of those concepts into a computational or mathematical object language. The “ontology log” or olog has the possibility for such a framework. The olog metalanguage can be used to represent models and data with mathematical sets and functions—set semantics. Applying this rigor opens a warehouse of mathematical tools available through Applied Category Theory.
References
[1] The Cambridge Encyclopedia of Language; David Crystal; 2010; page 254. [2] Knowledge Representation: Logical, Philosophical, and Computational Foundations; John F. Sowa; 2000; page 51. [3] Introduction to Symbolic Logic and its Applications; Rudolf Carnap; 1958; page 79. [4] How to Design Programs (Second Edition); Matthias Felleisen, Robert Bruce Findler, Matthew Flatt, Shriram Krishnamurthi; 2018; pages 78–80. [5] Category Theory for the Sciences; David Spivak; 2014; pages 184–188. [6] Ologs: A Categorical Framework for Knowledge Representation; Spivak & Kent; 2011. [7] Structure and Interpretation of Computer Programs; Harold Abelson, Gerald Jay Sussman with Julie Sussman; 1996; pages 140 & 359. [8] nLab (Wiki), “applied category theory”; last updated Oct. 2022. [9] Category Theory for the Sciences; David Spivak; 2014. Material for the rest of the article comes from page 204 (Section 2.3) and page 208 (Section 4.5). [10] Ologs; op. cit. [11] nLab (Wiki); “internal logic”; last updated March 2023. [12] Ologs; op. cit.




