By Mark R. Shapland
There’s a paradigm shift underway in benchmarking unpaid claims. Nearly every far-reaching decision any insurance entity makes—from pricing to capital needs and risk management—hinges in some way on projections of unpaid claims. Yet these estimates typically are prone to considerable variability.
To manage some of this uncertainty, actuaries increasingly have adopted the use of stochastic models to estimate distributions of unpaid claims. However, even these approaches cannot fully contemplate the randomness of future losses and unanticipated events. Without a point of reference, the loss-reserving process can fall victim to a number of complex phenomena. Moreover, no tool can steer an entity entirely clear of the risks of loss reserving. Advances in benchmarking unpaid claims, however, can provide a basis for comparison and a point of departure for understanding the reasonability of an entity’s unpaid claim estimates.
In projecting loss payments, actuaries are guided by a number of standards of practice regarding the appropriateness and reasonableness of a model and the need for multiple models to address model risk. However, the nature of unpaid claim estimation also presents actuaries with random outcomes and issues that require judgment and interpretation. Indeed, a lack of granularity and the length of time for which data is available unintentionally can mar output of the best models. These limitations can produce unpaid claim distributions that miss the mark on estimated future liabilities. Estimating unpaid claims also can fall victim to the tendency to assume, or hope, that the actual outcome will be “better than expected.” We intuitively may understand that “worse than expected” outcomes are far from unusual, but the tendency to see the “better” parts of the data and overlook the “worse” elements can creep into model assumptions and bias estimates. In addition, the pressure to publish strong financial results can push initial expectations lower than they should be. Both tendencies inadvertently can sway modelling assumptions and unpaid claim estimates, so actuaries commonly use benchmarks to provide a reality check.
For decades, the practice of back-testing has given actuaries a way to look back to determine how well a particular method works with respect to estimating the average: under what circumstances does the paid chain-ladder method produce more accurate estimates than the incurred chain-ladder method and vice versa.
More recently, back-testing has expanded to include the stochastic models used to estimate distributions, but the data requirements for this type of testing are much more extensive because the variance is being tested in addition to the mean. The focus shifts to whether there really is a 10 percent chance that expected loss payments will, in fact, fall above the model’s estimated 90th percentile. Underestimating the width of the loss distribution long has been a challenge in many commonly used models whose assumptions can lead to underestimates of required capital, inadequate pricing, and many other problems.
Study after study has added to actuaries’ understanding of the appropriate use of different types of models, enhancing their ability to analyze reserve variability and assess the quality of different models. However, until recently there hasn’t been a benchmark that can indicate the quality of a loss distribution estimate. For the most part, traditional benchmarks have been limited in their functionality and underlying data.
Benchmarking 2.0
Using a new approach, actuaries can now benchmark loss development patterns, unpaid claim distributions, and correlations between segments, all of which can be used to compare results from an entity’s model to those of various benchmarks.
It’s a quantum leap in benchmarking unpaid claims. The advanced benchmarks are derived from extensive testing that involved running hundreds of thousands of simulations using each Schedule P line of business for more than 30,000 data triangle sets. These simulated outcomes were then compared to actual losses from Schedule P nine years later. While Schedule P data is part of regulatory filings in the United States and the data is U.S.-centric, the benchmarks are more about adjusting for model biases, and parameters are included to allow users inside and outside the United States to tailor the benchmarks to their particular situations.
Loss Development Patterns
Like traditional benchmarks, these newly developed guidelines include a feature that gives actuaries a way to compare their development patterns with industry patterns. This new generation benchmark, however, improves upon traditional benchmarks by providing the actuary with distribution information about the loss development patterns. For example, Figure 1 shows a comparison of loss development patterns—based on user inputs, the average pattern, and the 55th percentile—that an actuary might consider in an analysis of unpaid claims for commercial auto liability. While the pattern developed from the user’s inputs initially might appear to reflect a smooth development pattern, in this case a strong argument for smoothing becomes apparent when viewed with the incremental graph.
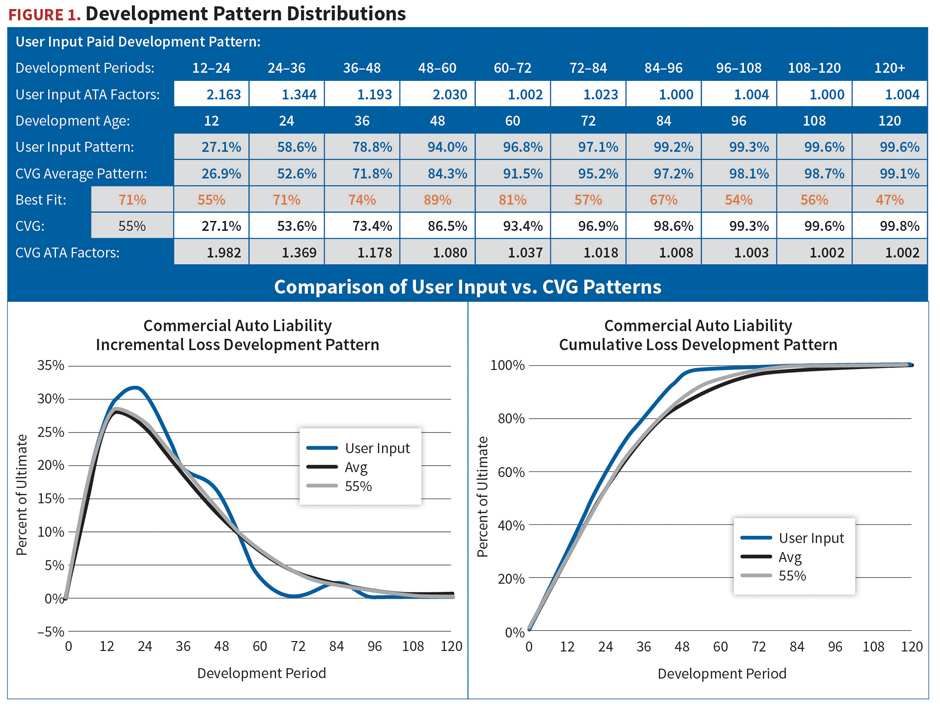
With this expanded tool, the actuary has the ability to check which percentiles produce the best fit at different parts of the development pattern. In Figure 1, for example, the 71st percentile appears to be the best fit over the entire pattern, but the 55th percentile is the better fit at earlier and later points in the development of claims.
Rather than just relying on an average pattern, as traditional benchmarks do, the advanced guidelines give actuaries a benchmark from which to investigate claim patterns at different percentiles and better understand the differences in development patterns. Professional judgment in arriving at a selected development pattern still is an integral part of the process because no benchmark identically mirrors the specific risk profile of an individual entity. But these next-generation benchmarks enable the actuary to work with a broader array of patterns than just the average.
Once a development pattern is selected, the actuary can then easily create a range, as shown in Figure 2, by selecting the development pattern range—in this case patterns with a percentile rank 20 percent above and below the selected percentile rank pattern—and calculating new unpaid claim estimates. Using this process, deterministic point estimates and ranges can be improved using stochastically derived development patterns.
Unpaid Claim Distribution Benchmarks
Extensive testing with the database of more than 30,000 data sets provides a sense that common models frequently underpredicted the loss distributions, a systemic error that is adjusted for in the benchmark algorithm. Simulations for entities of all different sizes also indicate a need to adjust the benchmark distribution for entity size, highlighting a shortcoming of and providing a solution for the traditional benchmarking approach, which only focuses on average development patterns and lacks the robustness of the uncertainty information.
Regression models were used to fit the distributions by premium volume for unpaid claims by accident year, calendar year, calendar runoff, and loss ratio distributions. Fitted results by premium volume were then smoothed to achieve consistency among distribution types and conformity with statistical properties.
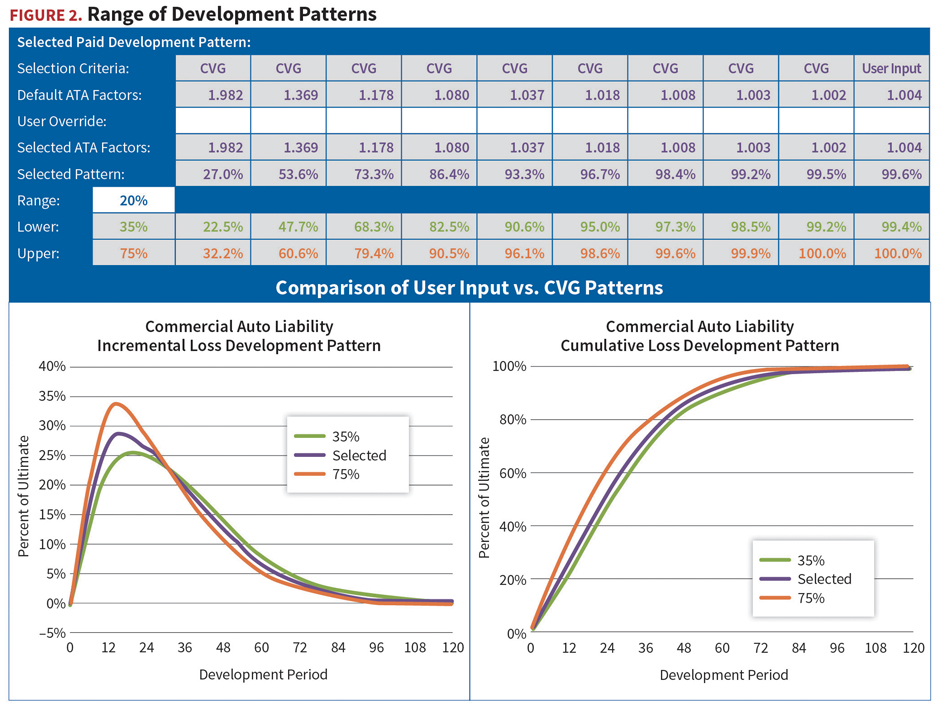
This back-testing and regression modelling resulted in the development of an algorithm that can be used to adjust unpaid claim benchmarks to account for entity size. Users input the entity’s premium volume and loss ratio data by accident year. The algorithm then calculates benchmark outputs for the mean and standard deviation, customized for the specific characteristics of the subject entity.
An example for commercial auto is shown in Figure 3, which illustrates the output for entities of two different sizes. While loss ratios are identical, the premiums and unpaid claims for the large entity are roughly eight times those of the small entity. However, the standard deviation for the large entity is only roughly five times larger than that of the smaller entity. Thus the coefficient of variation, the mean divided by the standard deviation, is smaller, indicating that the dispersion around the mean is narrower for the larger entity. Statistically, this conforms to the law of large numbers.
Early work with the benchmarks also suggested the need to give the actuary the ability to adjust the benchmarks to reflect their selected development patterns. In addition, the algorithm also can adjust for other factors, such as currency exchange to support international use.
In providing another frame of reference, the benchmarks add a level of comfort in knowing that an entity’s estimated output aligns with objective, tested metrics that have been thoroughly vetted for the possibility of underestimating future losses—one of the most common shortcomings in many models. Further, the collective benchmarks provide evidence to challenge or support the underlying data and assumptions used in modelling and provide a powerful tool to help guide actuaries’ professional judgment in determining the reasonableness of their analyses and a means of evaluating the quality of stochastic unpaid claim distribution estimates used in enterprise risk management (ERM).
Correlations Become a Reality
Identifying and quantifying correlations among segments has been a challenge for individual entities, which typically lack any benchmarks to compare to the correlations observed. This understanding of correlations among segments is critical in the process of forming conclusions regarding aggregate unpaid claims.
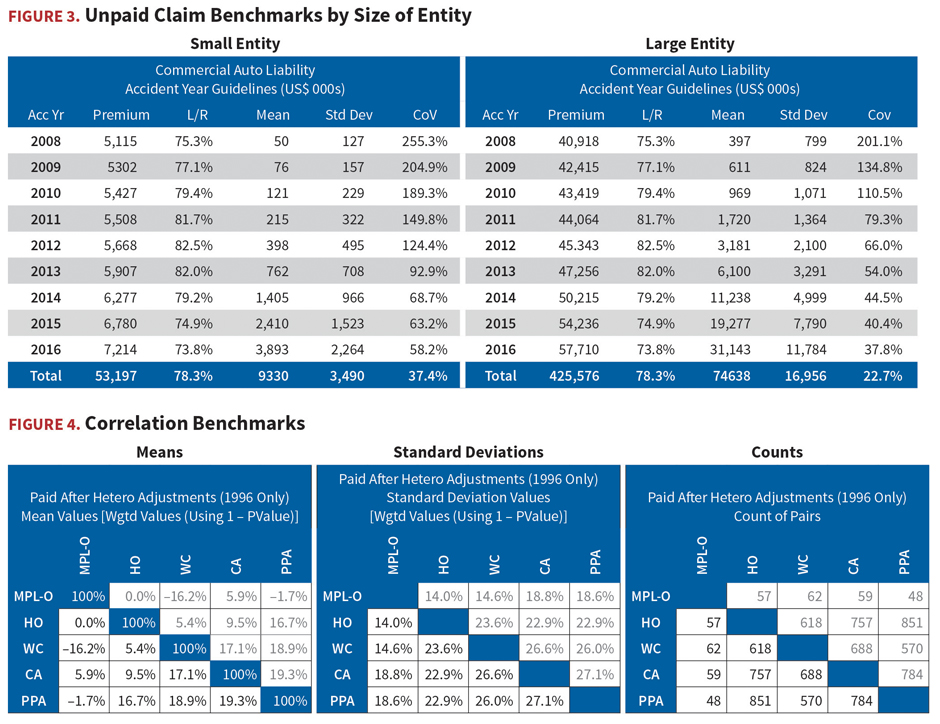
This is because an aggregate distribution of unpaid claims can be much narrower than the sum of the individual segment distributions, especially if the segments enjoy a large degree of independence leading to a diversification benefit. Alternatively, the difference between the correlated aggregate and the sum of the segments can be minor if the segments have a strong positive correlation. In either case, the effect on capital needs and reinsurance requirements can be substantial.
Advanced benchmarks allow for a better understanding of an entity’s estimated correlation. The back-tested output also includes correlations for all pairs of an entity’s lines of business for both paid and incurred claims. As the example in Figure 4 shows, actuaries can benchmark correlations for their entities based on their lines of business. The estimated correlations together with the underlying uncertainty, based on the robust industry data, give actuaries the ability to more confidently aggregate loss distributions, advise on risk and capital management issues, and potentially reduce volatility. These components are necessary for management to move confidently ahead with its strategic objectives.
While machine learning may someday increase the ability of actuaries to anticipate the randomness of future loss developments, today’s modelling techniques can fall short. For now, estimating unpaid claims requires actuarial deliberation and professional judgment. But this reality doesn’t negate the need for ever-more sophisticated tools that promote a more robust loss-reserving process, which can facilitate a wide array of benefits, such as:
- risk-based capital that is adequate to support operating activities;
- a close match between reinsurance needs and the entity’s risk profile;
- improved compliance with board-determined risk management guidelines;
- accurate assessment of risk margins for technical provisions; and
- more accurate product pricing.
The ability to benchmark an entity’s results against others in the industry and the industry as a whole can provide significant insights into both actuaries’ daily work and their strategic planning. Using the most advanced benchmarks available can help to ensure a more efficient integration of reserve variability analysis into ERM processes and enhance an entity’s strategies.
Mark Shapland, MAAA, FCAS, FSA, is a principal & consulting actuary with Milliman, specializing in P&C reserving and advanced stochastic modeling. He can be reached at mark.shapland@milliman.com.





