Probabilistic and statistical fallacies—how to spot them, and how to avoid them
By Carlos Fuentes
“Darius was already coming down to the cost from Susa, exalted in spirit by the magnitude of his forces and also encouraged by certain dream, which the Magi interpreted in a way to please him rather than as the probabilities demanded”
—Plutarch, “Lives—Alexander”
Probability and statistics are analytical tools with applications in many areas of knowledge. Unfortunately, for evolutionary reasons, our sense of probability and our ability to interpret patterns are poor:[1] our thought process struggles with large numbers; we are influenced by frames of reference; our choices are inconsistent; our views about gains and losses are asymmetric.
This article discusses several situations that challenge our analytical abilities. Each problem is easy to understand but the correct solution is counter-intuitive, as in The Monty Hall Problem and the Simpson’s Paradox, or the proper analysis requires distinguishing between randomness and order, as in finding interpolating curves, a task in which most of us struggle.
Probabilistic Fallacies
“Ignorance gives one a large range of probabilities”
—George Eliot, “Daniel Deronda”
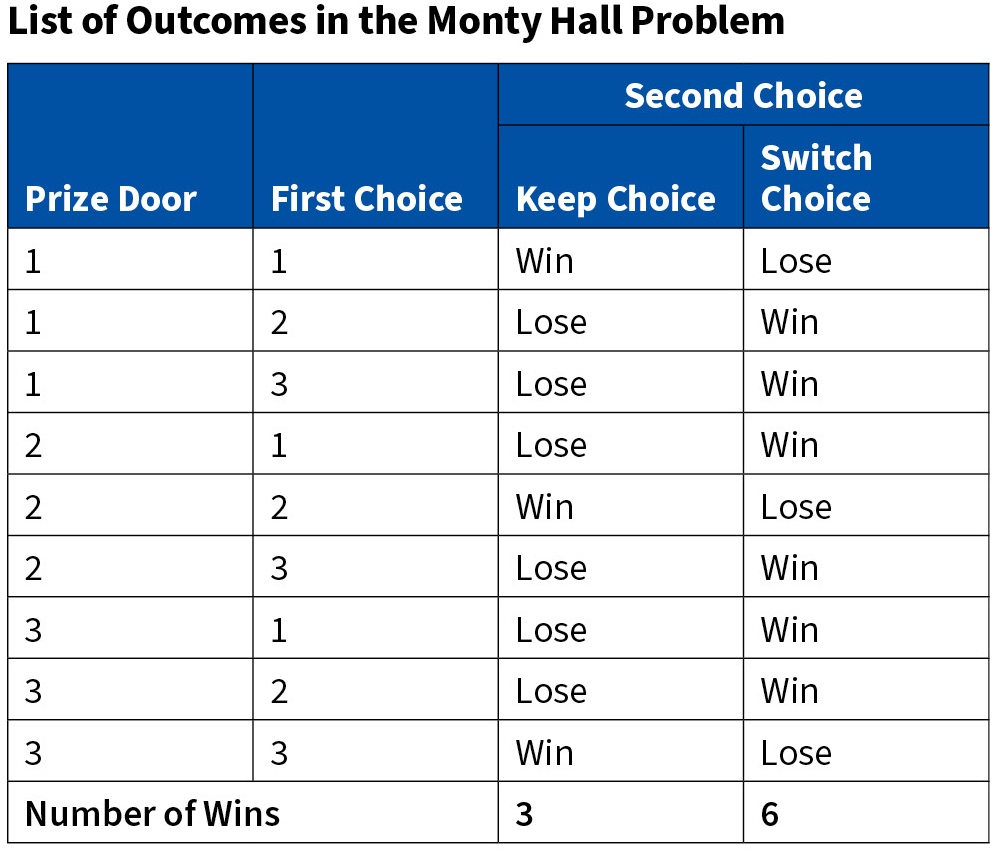
Avoiding probabilistic traps can be difficult, even for the trained professional. Consider the “The Monty Hall Problem”[2] in which a participant is asked to choose one of three doors knowing that there is a prize behind one of them. Once she has selected a door but before she knows whether her selection is correct, the host opens one of the remaining two doors making sure there is no prize behind it.[3] The host then gives the participant the opportunity to keep her choice or switch door. Does choosing a different door affect the probability of winning the prize? In fact, it does. If the participant does not change her mind the probability is 1/3; if she changes her choice the probability is 2/3. How can this be? To convince ourselves that these probabilities are correct we enumerate the outcomes in the following table on page 26.
The prize is in one of the three doors; the player can choose any of them. This means that there are nine combinations. Assume that the prize is in door 1. The following courses of action are possible:
1. If the player chooses door 1 thena. She wins if she keeps her choice
b. The remaining two doors do not have the prize. The host can open any of them
c. The player loses if she changes her choice
2. If the player chooses door 2 then
a. She loses if she does not change her choice
b. Either door 2 or door 3 has the prize. The host must open the door that has no prize
c. The player wins if she changes her choice
3. If the player chooses door 3 then the situation is similar to the case where she chooses door 2.

Analogous reasoning applies when the prize is in door 2 or in door 3. This means that there are three cases in which the player wins if she keeps her choice and six cases in which she wins if she switches door. In other words, the probability of winning without changing choice is 3/9, and the probability of winning by switching doors is 6/9.
In short, if the player picks correctly the first time and switches, she wins with probability 0%; if the player picks incorrectly the first time and switches, she wins with probability 100%. The probability of choosing correctly the first time is 1/3; the probability of choosing incorrectly the first time is 2/3. Thus, the probability of winning by switching is 2/3 = (2/3) × 1.00 + (1/3) × 0.00.
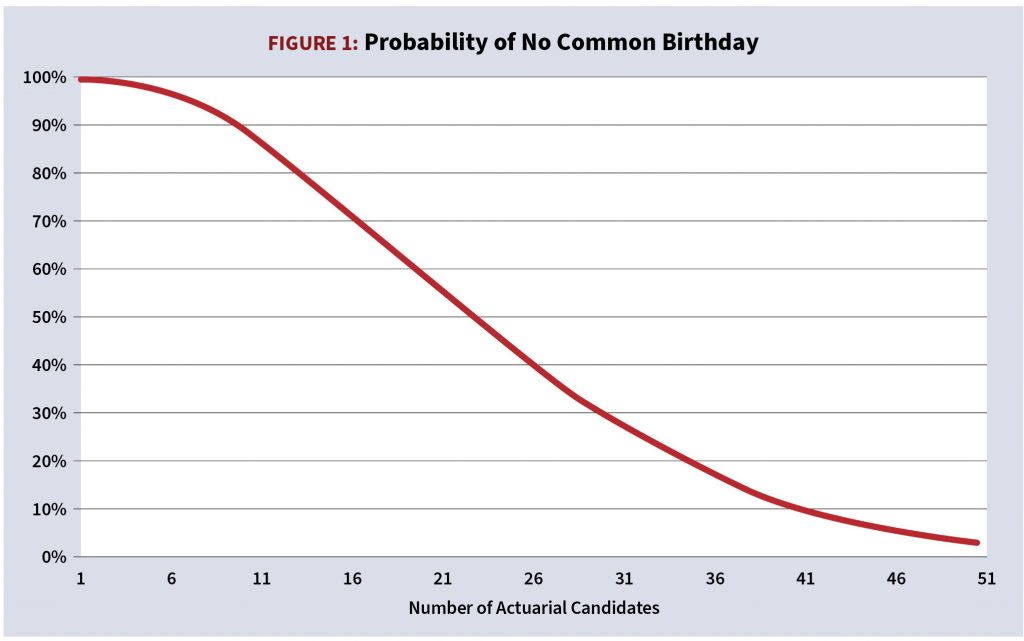
The birthday problem also illustrates our lack of probabilistic intuition: how many actuarial candidates are required to be present in a test center so that the probability that two or more of them share the same birthday is at least 50%? Most people guess 100 or more but the answer is 23.
Here is the solution: Let pn be the probability of no common birthdate among n candidates. This means that:
- If there are two candidates in the room the first person can be born any day of the year, but the second must be born on a different day, that is, the second person can be born in any of 364 days of the year. Thus, the probability of different birthdays is
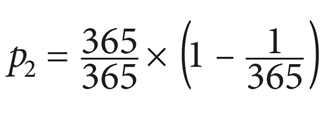
- If there are candidates in the room the probability of different birthdays is
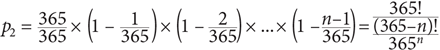
The numeric solution to the equation pn ≅ 0.5 is n = 23. In fact, the probability of a common birthday grows quickly, reaching 41% with 20 candidates, and 71% with 30. The tables that appear below provide details.
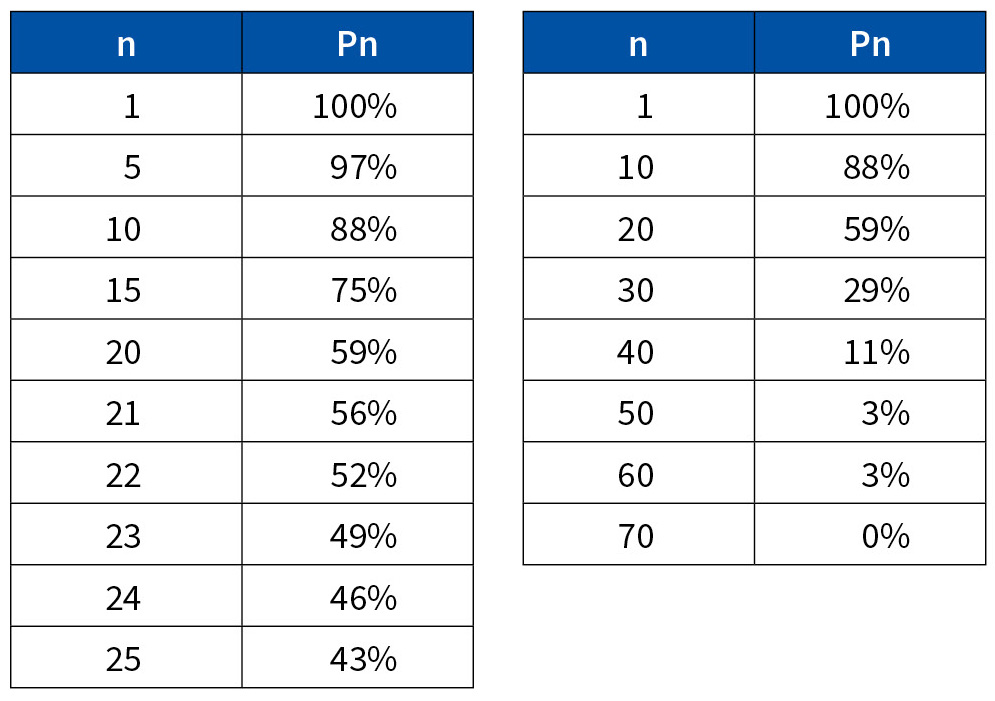
Figure 1 illustrates the evolution of the probability of no common birthday. It slopes downward quicker than most people think it should.
The analytical solution is complicated but it becomes manageable with a couple of simplifying assumptions.[4] Start with the Taylor series of the exponential function:
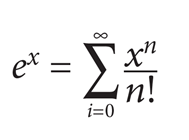
From the first order approximation
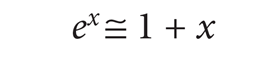
it follows that
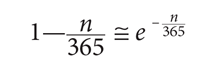
Thus, the approximation to the equation to solve is
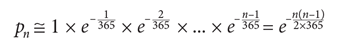
The additional simplification n(n—1) ≈ n2 leads to
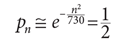
(1/2 is the desired probability). Taking the logarithm of both sides and simplifying yields n ≅ 23:

The root of many fallacies is our poor innate sense of probability, especially with large and small numbers. We notice coincidence and patterns that are the result of randomness but attribute causality to them. For example, you may think about a school friend you have not seen for a long time. When you see her, a few hours later, waiting in line next to you at the airport you may be tempted to believe that you have psychic power. If you do, you are like most of us. Attributing causality to this event requires ignoring the millions of random events that take happen in your life—dreams, cloud shapes, the first page of the book you opened yesterday, the last name of the person speaking when you turned on the TV, the plate of the car that crossed in front of you when you were driving to work, the lyrics of the music of your favorite song, etc.
Some people believe that winning the lottery cannot be the result of chance. After all, the probability of Joe Doe winning it is 1/100,000,000. But the fact of the matter is that the probability of someone winning it is high. Yet, the astrologer predicted Joe’s win or knew about it. How can this be? Well, theastrologers extracted information from Joe by making use of cold reading.[5] Joe not only shared personal information with the astrologer but helped him by falling prey to confirmation bias.[6] In short, the astrologer extracted information from Joe and made many predictions, but Joe remembered only those that were correct.
Furthermore, Joe ignored (or did not understand the role of) chance and manufactured mental connections that confirmed the astrologer’s psychic abilities.
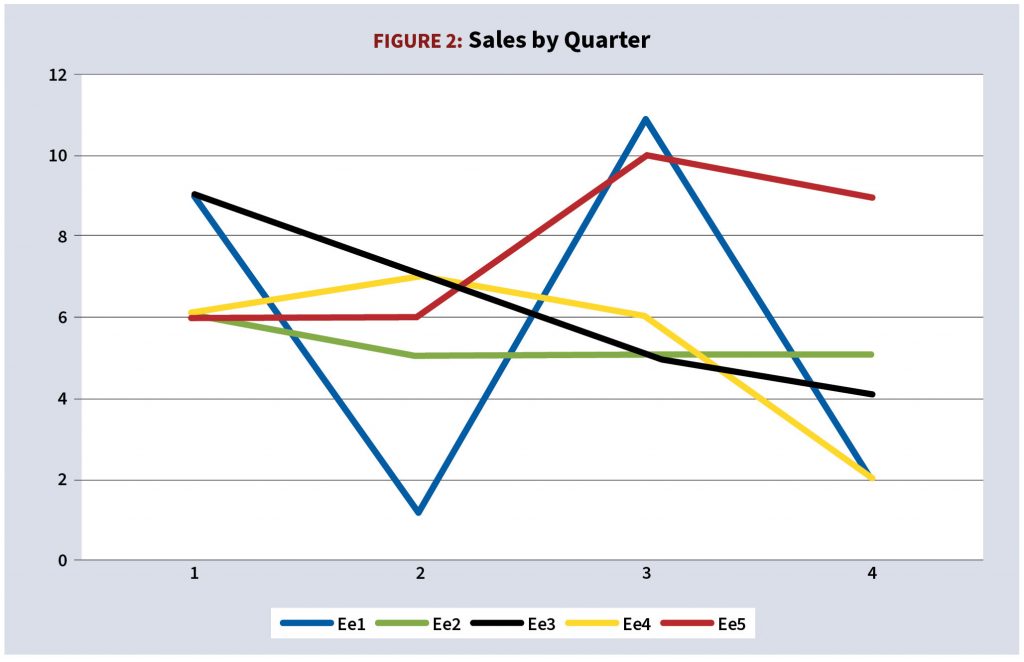
Consider next the problem of incentives to a sales force with the record depicted in the following chart. The sales team is part of a high-performing organization that prides itself for rewarding top performers and weeding out mediocrity. The sales staff is likely to receive reviews along the following lines (See Figure 2.):
- Employee 1 has potential but is inconsistent. He needs to improve his personal skills. No bonus;
- Employee 2 is consistently mediocre. He needs to improve his personal skills. Under probation. No bonus;
- Employee 3 had a good start but her performance declined steadily. She needs to improve her personal skills. No bonus;
- Employee 4 may have potential. His performance declined in the last two quarters. He needs to improve his personal skills. No bonus;
- Employee 5 has improved over time and ended the year with more sales than anybody else. She deserves a bonus. She will train the workforce.
Are these assessments fair? Certainly not because the number of sales is derived from the function
1 + 10 rand[0,1]
where random[0,1] is the random functions in the range [0,1].
In the real-world the performance of sales professionals is influenced by chance. Because determining whether the influence is small or large is a complicated matter, most of us ignore it.
The excellent paper “Framing, Probability Distortions, and Insurance Decisions” authored by Professors Johnson, Hershey, Meszaros, and Kunreuther provides several interesting examples of inconsistencies in the use of probabilities. They describe the following situation: you are going to travel from the US to a country that has experienced acts of terrorism. You can purchase one of following three types of travel insurance that pays a $100,000 death benefit during the flight: (1) from the US to the destination; or (2) from the destination back to the US; or (3) round trip. Two groups of Wharton Executive MBA students, expected to travel to that destination, were asked how much they were willing to pay for the insurance.
Let the insurance costs be c1 (from the US to the destination), c2 (from the destination back to the US), and c3 (round trip). Most readers would agree with the following two statements: c1 = c2; c3 =2c1 = 2c2. Here are the responses of the students:

Why are people willing to pay more for one leg of the trip than for the round trip? The answer has to do with how we construct scenarios in our minds and use them to estimate probabilities:
- Flights traveling to the US are more likely to be the targets of terrorist attacks than flights originating in the US (although this assumption can be correct, it relies on mass media reports, not on an analysis of relevant statistics), thus
- Thinking about the entire trip suggests pleasant images such as meeting new people, socializing with peers, sightseeing. The perception of risk diminishes, thus c3 < c1 + c2 and, more strikingly, c3 < c2.
The Ellsberg Paradox[7] also illustrates inconsistent choices. Consider the following experiment: there are two urns that contain balls of different colors as follows:
- Urn A contains 50 black balls and 50 white balls;
- Urn B contains 100 balls, some black, some white. The number of black (and white) balls is determined randomly.
Lulu is asked to choose an urn and a color. Then she is asked to draw a ball from the chosen urn. If the ball matches the chosen color Lulu wins a prize. What urn and what color should she chose? The answer is, of course, that it does not matter: the probability of winning the prize with either choice of urn and with either choice of color is 50%. But most people strongly prefer urn A and either color, say black. The marked preference for urn A makes no sense. If Lulu chooses black in urn A then she ought to believe that the probability of selecting black in urn B is less than 50%. This implies that Lulu must believe that the probability of choosing a white ball in urn B is greater than 50%. Therefore, Lulu should have chosen urn B and white. But she did not.
Finally, consider the following situation: Michael was a quarterback in college. Which of the following two statements is more likely to be correct? (i) Michael is a librarian, or (ii) Michael is a librarian and coaches the local high school football team. The connection between Michael’s days as quarterback and his role as a football coach leads most people to believe that the second choice is more likely to occur than the first, that is, that P(A) < P(A∩B), which is false.

Statistical Fallacies
“If your experiment needs statistics, you ought to have done a better experiment”
—Ernest Rutherford
Statistical fallacies are common and old. This section presents a few interesting cases.
The Simpson-Yule Paradox[8] occurs when the total marginal association between two variables is different from the partial marginal association between the same two variables. An example will illustrate: the table below shows the number of admissions and the number of large claims by unit for Hospital A and Hospital B. The portion of admissions that generate large claims is higher for Hospital B in all medical units (See Figure 3):
- In cardiology, 6.2% of the admissions trigger large claims in Hospital A and 8.3% in Hospital B;
- In oncology the percentages are 6.3% and 8.0%, respectively;
- In traumatology 2.9% and 3.5%;
- In intensive care 0.8% and 1.%.
The conclusion is that in each of the four medical units, large claims as a proportion of admissions is always greater in Hospital B than in Hospital A, that is,
Large Claims (%)Hospital B,Unit i > Large Claims (%)Hospital A, Unit i
for i = 1, 2, 3, 4.
Under these conditions, it is reasonable to conclude that in the case of combined medical units, large claims as a proportion of admissions are also greater in Hospital B than in Hospital A, that is,
Large Claims (%)Hospital B > Large Claims (%)Hospital A
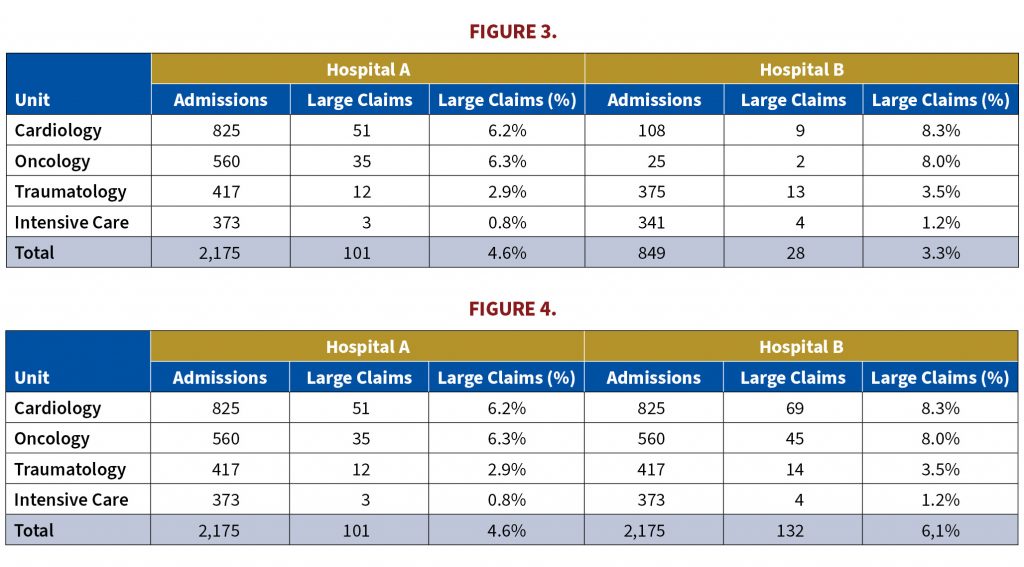
But to the surprise of many of us, the opposite is correct: the portion of admissions that generate large claims is now higher in Hospital A (4.6%) than in Hospital B (3.3%), that is,
Large Claims (%)Hospital B < Large Claims (%)Hospital A
Why the inequality, which points in the same direction for each medical unit, reverses direction when admissions and number of large claims are added over the four medical units? The reason is that the sizes of the medical units are different. For example, the number of admissions in oncology are 560 and 25 for hospitals A and B respectively, and the number of large claims 35 and 2. Put differently, the total is a weighted average, but the weights are different for each hospital. When the weights (or the number of admissions) are the same the direction of the inequality is the same for each medical unit and for all medical units combined, as shown in Figure 4.
The phenomenon of overfitting is easy to understand but in practice difficult to assess and even more difficult to resist because we believe, incorrectly, that the more complexity in the model, the better it is. Overfitting consists of developing a model that fits data closely. But overfitting typically does not capture data subtleties; instead, it incorporates random variations that compromise the model’s explanatory power and its forecasting ability. Overfitting has become a significant problem due to growing availability of data.
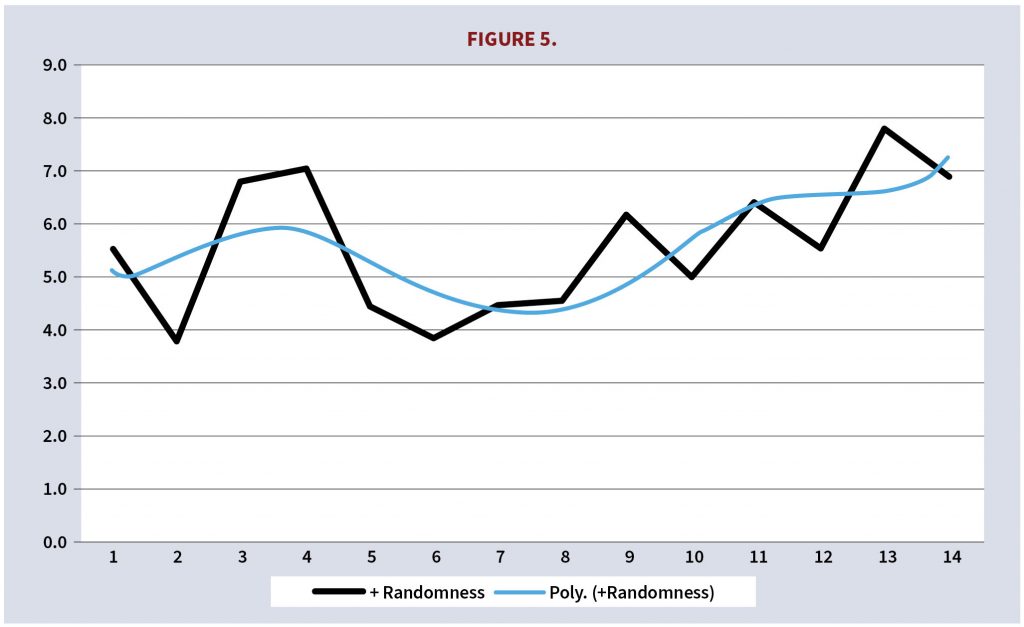
Consider the following typical problem: in Figure 5 the black line represents data; the blue line is the interpolating model, whose equation is
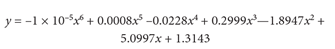
However, the equation that generated the data is
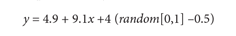
Therefore, the best approximation is the much simpler linear equation
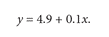
Figure 6 shows the data, the linear equation, and the polynomial. The polynomial fits the data better than the linear equation because it incorporates random variations.
But random variations are misleading. Consider the following graph, which is generated from the same linear equations with random variations (see Figure 7).
Once again, the polynomial fits the data better than the linear equation and gives the illusion of accuracy. Ideally, the two polynomial approximations should be about the same but instead they are significantly different in their explanations of the past and their predictions, as attested by the preceding two graphs and the following table which shows projected values one and two periods ahead.

The polynomials are different because the underlying data changed due to the random function 4 (random[0,1] –0.5). Random fluctuations cannot be explained or predicted.
In practice the second polynomial would be discarded because its projections look unreasonable. It would be more difficult to conclude that the projections of the first polynomial are incorrect even though they are, as shown in Figure 8. A more common approach would be to adjust the polynomial to reduce the growth and maybe add some random variation but doing so complicates the model (which makes it credible to some) and misleads by suggesting that growth is exponential instead of linear.
The fact of the matter is that we must fight our innate tendency to assign causality to randomness but doing so is an uphill battle.
Statistical fallacies may be based entirely on concepts. The predictions of Nostradamus,[9] written in quatrains[10] to give the illusion of mystical depth, illustrate the dangers of using data mining[11] to justify unfounded credence. Take Quatrain 2-10 from “Les Propheties”:
Before long, all things will be controlled,
We shall endure a time very sinister;
The status of artists and their independence greatly changes,
Few will be found who will want to be in their place.
By retrofitting, that is, by mining data and finding a pattern, it is possible to ascribe meaning where none exists. In this case, a great number of people believe that Nostradamus predicted the emergence of Nazism. But the prediction is as general as it is useless—the reader can easily ascribe meaning in accord with his own beliefs. Not surprisingly, the few predictions in which Nostradamus was specific turned out to be resounding failures. Take quatrain 10-72:
The year 1999, seventh month,
From the sky will come a great king of terror;
To bring back to life the great king of the Mongols,
Before and after mars to reign by good luck.
The person who believes Nostradamus prophesies can mine his own data and make assumptions to justify anything. He may state that the world did not come to an end in 1999 because the starting point should have been the year 30, or 50, or by assuming that a year consists of 400 days, or by some other device that it will never fail to convince certain groups of people.
Here are two additional examples of statistical fallacies:
The Sports Illustrated Curse[12] refers to the belief that athletes who appear on the cover of the magazine see a decline in their performance. But such declines almost always can be explained by the phenomenon known as regression to the mean;[13]
People generally believe that a basketball player is on a streak when she is performing above average, but studies show that the observed pattern is almost always the result of randomness.[14]


Concluding Remarks
“Statistics are no substitute for judgement”
—Henry Clay
Probabilistic and statistical fallacies are ubiquitous. Those that arise in science are subject to expert scrutiny and are resolved eventually, but most fallacies occur in our daily interactions and although biases can be mitigated[15] poor decision making is pervasive in society. Decision-makers are influenced by fallacious thinking as much as the rest of us. The consequences range from the trivial to the vitally important.
CARLOS FUENTES, MAAA, FSA, FCA, is president of Axiom Actuarial Consulting. He can be reached at carlos-fuentes@axiom-actuarial.com.
The opinions expressed in this article are the sole responsibility of the author They do not express the official views of the American Academy of Actuaries, nor do they necessarily reflect the opinions of the Academy’s officers, members, or staff.
Endnotes
[1] See “Predictably Irrational,” Contingencies Jan/Feb 2020, p. 17 [2] See “The Monty Hall Problem: A Statistical Illusion” by Jim Frost, https://statisticsbyjim.com/fun/monty-hall-problem/ [3] If the participant’s choice is correct, the other two doors have no prize, so the host can select either. If the participant’s choice is incorrect then the prize is behind one of the remaining two doors. The host selects the door with no prize. [4] The theoretical estimation of the difference between the exact solution and the two approximations described below requires a level of mathematical sophistication that goes beyond the scope of this article. However, the approximate solution is remarkable close to the exact solution. [5] Cold reading refers to gaining information using a series of tricks and psychological manipulations. If done skillfully, the subject is unaware that he revealed the information himself. See “Cold Reading Techniques (Powerful Techniques to Wow the Crowd” in https://www.thementalismcourse.com/cold-reading-techniques-powerful-techniques-to-wow-the-crowd/. [6] The tendency to look for information that supports one’s preconceptions, typically by interpreting evidence to confirm existing beliefs while rejecting or ignoring any conflicting data. [7] Daniel Ellsberg (1931-) is an American economist, political activist, and former military analyst. In 1971 he leaked portions of a classified report that detailed the history of the US intervention in Indochina from World War II until 1968. The report undercut the publicly stated justification of the Vietnam War. [8] Edward Hugh Simpson (1922-2019) was a British codebreaker, statistician, and civil servant. George Udny Yule (1871-1951) was a British statistician. [9] Michel de Nostredame, Latinized as Nostradamus, (1503 to 1566) was a French astrologer, physician, and reputed seer. He is best known for his book “Les Propheties,” a collection of 942 poetic quatrains. [10] A quatrain is a simple poem with four lines. Nostradamus’ quatrains were written in French with some Italian, Greek, and Latin. He enhanced the faux mysticism that permeates his writings by swapping, adding, or removing letters of proper names. [11] Data mining is the process of finding anomalies, patterns, and correlations within large data sets to predict outcomes. Such findings require verification. Data mining is a legitimate analytical tool that can be, and frequently has been, abused. [12] See “The Sports Illustrated curse and regression to the mean” by Briggs on September 24, 2010, https://wmbriggs.com/post/63/. [13] Regression to the mean is the process under which, over repeated sampling periods, outliers tend to revert to the mean. [14] See “That’s So Random: Why Persist in Seeing Streaks,” New York Times, June 26, 2014, https://www.nytimes.com/2014/06/26/science/the-science-of-hot-hand.html [15] See “Framing, Probability Distortions, and Insurance Decisions” by Johnson, Hershey, Meszoras, and Kunreuther.




