The SuperContest

By Josh Feldman

As cold temperatures and polar vortexes hit large swaths of the country, the days of watching outdoor cross-country meets seem like a distant memory. But luckily for us running fans, the competition only heats up once winter comes along, as indoor track season is about to get underway!

For those of you who thought gambling on cross country meets was intense, well, the stakes only get greater once the runners head to the 200 meter indoor oval. If you listen closely to fans in attendance at any indoor track meet, you are bound to come across some gambling talk. Each event is just a new excuse to gamble your hard-earned dollars away (or as the glass-half-full people would prefer to say, each event is an opportunity to invest your hard-earned dollars in some of the best athletes in the world).

When it comes to indoor track, one gambling event shines above them all: the SuperContest. Tales of the SuperContest have become legendary to pro and aspiring gamblers alike. In this great gambling event, each person wagers $1,500, and each week each entrant picks five teams that they think will be victorious that week. For each team you correctly pick, you get a point. After 17 weeks, the person with the most points wins the SuperContest—and all the fame and prize money that accompany the title. While it is theoretically possible to amass 65 points (65=17*5), most years the winning entry scores a lot less.

For years I dreamed of entering the SuperContest, and for various reasons I never did pull the trigger. But this year will be different. I will not only enter the contest, but with my superior math and running knowledge, I am going to take the crown as well!

With the first week of the contest just days away, I decided to talk to my old gambling buddy Chef about proper strategy needed to win the contest. After helping Chef with booking the big cross-country meet a couple of issues ago, I felt he owed me some advice.

As it turned out, Chef truly was a wealth of knowledge about the SuperContest. He told me that each year entries are capped at 500 participants, and they always sell out. He also told me a lot about the intricate scoring of indoor track meets, and how ties get broken so that each meet has one distinct winner. Overwhelmed at all the information, Chef finally told me the important knowledge needed.

First, he said that there are literally hundreds of indoor track meets that you can choose from. Each meet has only two teams, and all you have to do is pick the winning team. He also said that indoor track is the most random of sports, and that no matter who you are, no one can pick a winner with more than 50 percent accuracy. Finally, he told me that last year’s contest winner managed to have more wins than losses each of the 17 weeks. So your goal should be to do whatever possible to get at least three points each week of the season.

I guess I have enough information to get started, but it feels really hard to pick more winners than losers for 17 weeks in a row. Maybe my puzzle-solving friends can help put my thoughts into precise calculations for me…

1. Given all the information above, assuming each entrant truly is random and that no correlations are in play, what is the probability that at least one of the 500 entrants will pick more winners than losers in each of the 17 weeks of the contest?
2. Assume that I do indeed pick more winners than losers in week 1. What would my expected score in the contest be after the first week?
3. After the contest ends in 17 weeks, what is the median winning score of the SuperContest?
4. Assume that I defy all odds and somehow pick more winners than losers in each of the 17 weeks of the contest. What is my probability of winning the SuperContest?

Solutions may be emailed to cont.puzzles@gmail.com.

In order to make the solver list, your solutions must be received by March 31, 2019.

Solution to Previous Puzzles: Crossnumber Puzzles

A record (for me) 29 solutions, all completely correct (no partial credit), were submitted for this problem set. Does this mean the set was too easy? Or was it more attractive? One solver wrote, “Once I started I could not … stop.” Is that good or bad?

The problems; Fill a Crossword-like diagram with digits in each blank space so that that numbers formed satisfy given prime decompositions. No number has a leading zero and distinct primes are represented by distinct capital letters.

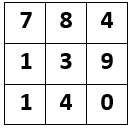
Problem 1: 3 by 3 square, i.e. 9 spaces formed into 3 rows and 3 columns. Across: 1, A⁴B². 4, C. 5. A²BD; Down: 1, E²F. 2, ACE. 3, AB²D.

Problem 2: 4 by 4 square, i.e. 16 spaces formed into 4 rows and 4 columns. Across: 1, AB. 5, ABC. 6, AD. 7, AC; Down: 1, BEF. 2, AG. 3, CH. 4, C⁴D⁴.

Problem 3: 4 by 4 square, i.e. 16 spaces formed into 4 rows and 4 columns. Across: 1, AB³C³. 5, D. 6, E⁵. 7, FE⁴; Down: 1, A²B³G. 2, BD. 3, AD. 4, AEH.

Answers: Problem 1:

Problem 2:

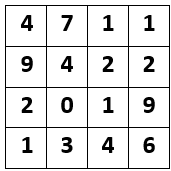
Problem 3:

Solutions: One method would be to try all sets of prime numbers to see what works, but this could take too long. So, we use mathematical insights to reduce the number of objects to test. Keep the following insights in mind when reviewing the following solutions. Mainly, a number, N, in any row or column is bounded: In problem 1, 100 ≤ N ≤ 999, in problems 2 & 3, 1000 ≤ N ≤ 9999. In addition, one needs to apply divisibility and that once a prime has been assigned to a letter it cannot be assigned to another letter in the same problem.

The solution steps below are very sketchy; they might be considered hints with answers. A complete set of discursive solutions would be longer than a main article in this magazine and repetitive. Of course, there are alternative ways to get the answers. Thanks to everyone who sent in their own solution sketches; I plan to study them for ideas on how to improve this type of problem.

PROBLEM 1

1. 2 Down & 4 Across ► AE=6.
2. 1 Across ► B = 5 or 7 ► A = 2 & B = 7 ► E = 3
3. 9 divides 1 Down ► F=79.
4. 3 Down, ► D = 5.
5. There are 10 possibilities for the central digit n; and (8n4)/6 is prime ► n = 3

PROBLEM 2

1. 4 Down ► CD=6►C=2 & D=3
2. 5 Across & 7 Across ►B<10,
3. 1 Across & 4 Down ► B ≠ 5 ►B=7 and A ends in 3
4. 5 Across and 7 Across ► 500 < A < 714
5. There are 10 primes ending in 3 between 500 and 714. Only one fits ► A=673.

PROBLEM 3

1. 6 Across ► E=5 ► F≤13.
2. 5 Across ► Case I:A = 3 & BC = 14 OR Case II 4 < A < 46 & BC = 6.
3. Case II & 3 Down ► A = 7 ► 1 Across = 1512 a contradiction.
4. ►Case I: 1 Across= 8232 ►B=2 ► C = 7 & 2 Down ► F=11.
5. There are 10 possibilities for the 2^nd digit n of 2 Down & (2n18)/2 is prime ► n = 0.