By Stephen Meskin
Recently, while my wife and I were visiting our son and his family, we decided to play a board game called Blokus. In this game, each of four players has an identical set of 21 pieces, differing only by color for each player. The pieces are placed on the board in turn until no one can continue. Each set of pieces is made up of the 21 different polyominoes of size 5 or less. (A polyomino of size n is a plane figure constructed by attaching n standard unit squares, side-by-side.)
There is one polyomino of size 1, called a monomino; one of size 2, the familiar domino; and two trominoes, five tetrominoes, and 12 pentominoes of sizes 3, 4, and 5 respectively. The five tetrominoes are shown just below. The letters underneath each are the names I have given them because they remind me of each tetromino’s shape.
Polyominoes have been used to pose problems and puzzles for over a hundred years. One type of puzzle is to ask people to tile a region with some set of them. Indeed, the first problem is to determine how many distinct ways one can tile a 4×4 square using tetrominoes. The tetrominoes used in one tiling can be all the same, some the same, or all different. We consider two tilings to be distinct if one cannot be made to look like the other by a sequence of rotations or flips about its horizontal, vertical, or diagonal axes. To get full credit you must exhibit each distinct tiling.
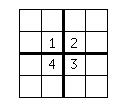
We will say a tiling is labeled if 1) each of the tiles of size n used in the tiling has its n unit squares labeled 1 to n; and 2) the same number in two different tiles of the tiling do not touch, not even on a diagonal.[1] The second problem is to count how many distinct labelings there are for the unique tiling from the first problem made up of four B-tetrominoes. We consider two labelings to be distinct if one cannot be made into the other by permuting the labels. Again, to get full credit you must exhibit each different labeling. But to make it possible to review your answers, they should all have labels 1, 2, 3, 4 arranged clockwise around the center starting from upper left. Thus, all answers to problem two must contain the following:
For the third problem, apply problem two to each of the distinct results from problem one. That is, for each distinct tiling you found in problem one, count the number of distinct labelings as described in problem two. Continue to keep 1, 2, 3, 4 around the center just as in problem two. However, I do not want to see each distinct labeling; I just want the counts of the number of distinct labelings for each distinct tiling from problem one—but make sure I know which count applies to which tiling.
If you like this sort of thing, you can of course try to generalize the puzzle to tiling other regions or using other sets of tiles; e.g., increasing the size of the polyominoes from 4 to 5 or higher or mixing sizes.
Previous Issue’s Puzzle: Tournament Time
What’s the probability of the 1 seed winning the tournament? The key is that you have to set up a three-level decision tree. The probability of the 1 seed winning its first game is 8/9. It has a 5/9 chance of playing the 4 seed in the second round, and a 4/9 chance of playing the 5 seed. So the probability of the 1 seed making it to the finals is: (8/9) × [(5/9) × (4/5) + (4/9) × (5/6)] = 72.4%. The 1 seed can potentially face the 2, 3, 6, or 7 seed in the final. Continuing this logic and filling out the decision tree (spreadsheets make this much easier) gives us a probability of 52.8% of the 1 seed winning the tournament outright.
What’s the probability of the 1 seed winning the tournament and covering the spread each game? The key here is that 50% of the time the favorite both wins and covers the game by definition. No matter what happens, the 1 seed will be the favorite in each of the three games it plays, and if the team covers the game, it automatically moves to the next round. So the answer here is simply 0.5 × 0.5 × 0.5 = 0.125.
Regardless of who wins, what’s the probability of the winning team covering each game it plays? Similar to part 1, you will have to set up a decision tree—not just for the 1 seed, but for all eight teams in the tournament. The first step is to set up the tree so that you determine the probability of each of the eight seeds winning the tournament outright. Next, for each branch of the decision tree where the favorite wins, replace the favorite’s winning percentage with 50%, as that’s the probability of that team covering. For example, when team 2 faces team 7 in the opening round, team 2 wins and covers half the time, wins yet does not cover 5/18 of the time, and loses outright 2/9 of the time. So we need to replace 7/9 (the probability of winning outright) with ½ (the probability of winning and covering). If the underdog wins, we don’t need to alter the formula, as they cover by definition. After doing the computations, the probability the 2 seed wins the tournament and covers each game is 15.8%, for the 3 seed it’s 6.7% … if you sum the probabilities for all eight teams, you get your final answer of 41.4%.
Solvers
Robert Bartholomew, Joel Barz, Bob Byrne, William Carroll, Brendan Cawley, Bob Conger, Andrew Dean, Andrew Dvorine, Bill Feldman, Yan
[1] The idea of labeling comes from a weekly puzzle in The New York Times Magazine called Capsules.