By Josh Feldman
I greatly disagree with the concept that you control your own destiny. Sure, there are plenty of things you control, but there are many events that impact your life that you have absolutely no control over. For a personal example, a few months before I entered the world, my dad started interviewing for full-time jobs, and had two good prospects. One big opportunity was in southern California; the other was in the “Show Me State.” If my dad took the job in Orange County, it’s clear my life would be very, very different than it is right now.
If I grew up in California, adjacent to the beach, I would have learned to surf at an early age. My whole childhood would have been devoted to catching waves, and before turning 20 I would have joined the World Surf League—the prestigious, professional tour of surfing. Instead of writing actuarial puzzles, I’d be out there on the tour performing better barrels than Gabriel Medina, having cooler hair than John John Florence, and offending more people than Mick Fanning. Ah, what might have been!
It’s virtually impossible to be a pro surfer without daily access to good waves, so my dreams died before they began when my parents ended up here in the great Midwest. We traded police chases, earthquakes, and fierce traffic for Blues hockey, toasted ravioli, and jokes about what high school you attended. Maybe we did get the better end of the bargain after all.
Even though I’m not a pro, I still enjoy watching the World Surf League on television. One of the enjoyments of watching is that surfing has one of the most mathematical scoring rubrics of any sport out there. For the uninitiated, most surf competitions have heats, where two surfers go head-to-head to see who is better. Heats usually last for 35 minutes, and although a competitor can ride as many waves as (s)he wants during those 35 minutes, only the sum of your top two scores count to see who wins. If your top two waves are a 7 and a 6, then you have a heat score of 13, no matter what took place on all the other waves. And thanks to the priority system, there is no “sharing” of waves; each wave gets ridden by at most one surfer.
A few days ago my friend Park and I started watching the latest stop on the World Surf League tour. Park made the comment that these surfers are so good, anyone out there can ride any wave, and it’s all pure luck who wins or loses depending on who rides which wave. Unfortunately, there’s a lot of truth to this comment, as the best in world can ride almost any wave that the ocean spits out. If a wave has a potential score of a 9, you’d better believe that any pro out there will score exactly a 9 on the wave. Not a point lower, not a point higher.
Of course, if I were a pro surfer, I’d have a secret plan. See, whereas most surfers are notoriously picky when it comes to which waves to ride, as a math person, I know it’s just a numbers game, and would make sure to ride at least one more wave during the heat than my opponent. The question then becomes: How would this impact my chances of winning a heat?
Let’s assume that I ride six waves in a heat, and my opponent rides five. Let’s also assume that it’s totally random and uncorrelated as to what the scoring potential of each wave is. Each wave has a whole-number scoring grade between 1 and 10, with 1 being the lowest score and 10 being the highest. It’s totally random and unknowable what the score of the wave will be beforehand, as there’s exactly a 10 percent chance it will be any number between 1 and 10. Given all of these assumptions, what’s the probability of me winning, losing, and tying the heat?
To further reward gnarly high scores, the Big Wave Tour slightly modifies the scoring system so your top wave counts double. Hence, if my top two scores are a 7 and a 4, my heat score is now 18 (two times 7 plus 4) instead of 11. If all the other assumptions from above still hold, what is the new probability of me winning, losing, or tying the heat?
Solutions to Polyominoes
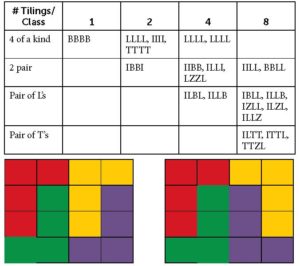
Problem 1: How many distinct ways can tetrominoes tile a 4×4 square? Two tilings are considered distinct if one cannot be made to look like the other by a sequence of rotations or flips about its horizontal, vertical, or diagonal axes.
There are 117 tilings of the 4×4 square using tetrominoes. They fall into the following 22 distinct classes:
The four-letter words in the table indicate the tetrominoes used in the tilings. Their order in a tiling starts at the top left, moves down the left border to the bottom, and then repeats. All I’s are vertical. Dividing into 8, the number of tilings for a class gives the order of its symmetry group. Sometimes two words are the same but, except in one case, they have an unequal number of tilings. The exception is the pair of LLLL classes, with four tilings each, shown on page 70. The most commonly missed tiling was the other LLLL, where the L’s appear to rotate the center.
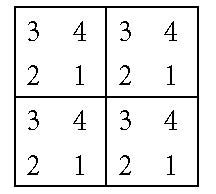
Problem 2: How many ways can BBBB be labeled by the numbers 1, 2, 3, 4 in each tile so that no two numbers meet, even on a diagonal, and that 1, 2, 3, 4 appear clockwise around the center box starting with top left of that box?
There are seven ways. The labeling of BBBB at right alternates two numbers in each row and column. Additional labelings arise by reversing the top row: T, bottom row: B, left column: L, or right column: R. But one can’t reverse a row and a column at the same time. There are thus six additional labelings: T, B, TB, L, R, and LR.
Problem 3: How many ways can all the tilings from Problem 1 be labeled as described in Problem 2?
There are seven for BBBB; one each for IIII, IBBI, and IIBB; and zero for the rest. Observing that no tiling can contain L gives the answer for 17 of the 22 tilings.
An oddity of these problems was that Problem 1 seemed to be the hardest and Problem 3 the easiest.