By Roy Goldman
It’s 1954 and air travel is quickly replacing rail travel. You are the chief actuary of the Insurance Company of North America [INA].[1] You are attending a Christmas party and your CEO, who is dressed in a Santa costume, asks you completely out of the blue, “What are the chances that two passenger planes will collide in midair?” Such an event has never occurred, so how do you answer such a question? For a more recent example, the chief financial officer of Humana asked me—after just one person died from Ebola in the United States—“What could the Ebola virus cost Humana in medical claims?”
In the November/December 2011 issue of Contingencies, James Guszca and Thomas N. Herzog published a book review of The Theory That Would Not Die by Sharon Bertsch McGrayne. Their review so captured my attention that I purchased the book at once. It is, indeed, a captivating book due to its rich compilation of historical issues as well as for the many vignettes of famous statisticians, mathematicians, and actuaries. Actuaries play such key roles throughout the book that it is worth an expanded review with special emphasis to actuarial contributions.
 Bayes’ Theorem
Bayes’ Theorem
The “theory” in the book’s title refers to applications of Bayes’ theorem, which is a fairly simple concept covered in undergraduate probability courses. Yet, it took nearly 200 years for the theory to be fully accepted, even though it had been used to solve a wide range of questions affecting society, the military, and medicine. Even after the theory was successfully used, it “went into hibernation” and had to be “rediscovered.” Often, it was an actuary who resurrected or republished the theory, as the leading statisticians thought the concept too heretical to be taught.
For hundreds of years, probability was thought to be a “doctrine of chances” or “frequency.” One repeats an activity many times (e.g., throwing dice) and then counts how many times a certain event occurs (e.g., throwing a 7 or 11 in a craps game). Some very famous statisticians that we all study (Karl Pearson, Ronald Aylmer Fisher, Egon Pearson, and Jerzy Neyman) were in this frequency camp. While they detested each other, their common enemy were the Bayesians, who believed that other relevant historical or prior information may be used to build model parameters. Sometimes a prior assumption was picked out the air, but it still led to useful outcomes. Such an assumption was considered anathema by the frequentists.
Returning to the question of airplanes colliding, a frequentist would tell the CEO of INA that the probability is zero because no midair collision had ever occurred. Fortunately, INA’s actual chief actuary, Laurence H. Longley-Cook, took a different approach. He found some data on general airline accidents and wrote on Jan. 6, 1955, “Other conditions remaining equal, we may reasonably expect anything from 0 to 4 [collisions] over the next ten years … the possibility of catastrophe is not so remote that it can be ignored [in pricing]. … Further, the protection of such an account by reinsurance … seems essential.”[2] Two years later there was such a catastrophe, and a second one occurred four years after that.
Actuaries today would say, of course, that’s what one would do to answer that question or the Ebola query posed by my CFO. But that was not always the case. As relayed in the book, frequentists ruled the academic world. It took individual actuaries and other practical mathematicians to reinvent Bayes’ theorem and apply it to solve problems in business problems, national security, and health care.
Thomas Bayes and Richard Price
Indeed, it was an actuary who published Bayes’ theorem in the first place. Bayes’ theorem is easily derived. Given two events A and B, with probability P(A) and P(B), what is the probability that both occur—P(A∩B)? One can think of this in two ways:
- If A occurs first, it’s the probability that A occurs times the probability that B occurs given that A occurs, or in symbols, P(A)P(B|A), or
- If B occurs first, it’s the probability that B occurs times the probability that A occurs given that B occurs, or in symbols, P(B)P(A|B).
Equating these expressions gives Bayes’ theorem:
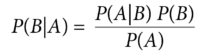
.
Bayes’ theorem relates to the application of this theorem by using assumptions for the right-hand side of the equation (called “prior assumptions”) to derive an updated or “posterior estimate” for the left-hand side. This “posterior estimate” becomes the next “prior assumption” for B, which leads to a more refined estimate for P(B|A).
 Bayes died before publishing his idea. His family asked his friend Richard Price to go through his papers. Price completely reworked and refined Bayes’ original essay and presented it to Great Britain’s Royal Society in a paper titled “An Essay toward solving a Problem in the Doctrine of Chances.” As a Presbyterian minister, he used the theory to prove the existence of a deity. This is the same Richard Price who became one of the first professional actuaries. He created the Northampton Life table and published the first major work on actuarial science.[3] Reversionary annuities still make great mathematics of life contingencies questions today!
Bayes died before publishing his idea. His family asked his friend Richard Price to go through his papers. Price completely reworked and refined Bayes’ original essay and presented it to Great Britain’s Royal Society in a paper titled “An Essay toward solving a Problem in the Doctrine of Chances.” As a Presbyterian minister, he used the theory to prove the existence of a deity. This is the same Richard Price who became one of the first professional actuaries. He created the Northampton Life table and published the first major work on actuarial science.[3] Reversionary annuities still make great mathematics of life contingencies questions today!
Price had a few other accomplishments as well. Quoting from McGrayne’s book, “the Continental Congress [asked] him to emigrate and manage its finances; Benjamin Franklin [nominated] him for the Royal Society; Thomas Jefferson [asked] him to write to Virginia’s youths about the evils of slavery; John Adams … attended his church. … When Yale University conferred two honorary degrees in 1781, it gave one to George Washington and the other to Price.” Now that’s a résumé.
 Credibility Theory:
Credibility Theory:
an American Invention
The famous mathematician Pierre Simon Laplace is the one who developed the language and structure for deriving Bayes’ theorem. He used it to solve military and celestial problems as well as to show how little confidence one should have in using a witness’s testimony in a jury trial. Laplace also developed the central limit theorem; named the meter, centimeter, and millimeter; and served for a short time as Napoleon’s interior minister. Unlike Price, however, when Napoleon complained that “Newton spoke of God in his book. I have perused yours but failed to find His name even once. Why?” Laplace replied, “Sire, I have no need of that hypothesis.”[4] Laplace influenced probability theory for over a century. For him, “essentially, the theory of probability is nothing but good common sense reduced to mathematics. It provides an exact appreciation of what sound minds feel with a kind of instinct, frequently without being able to account for it.”[5]
But there arose problems that intuition couldn’t explain, and critics began complaining about his rule. For example, in the United States between 1911 and 1920, states began requiring employers to insure workers against occupational injuries and illness. Insurance premiums had to be formulated for every large company. Data were scant. Isaac Rubinow, a physician and statistician for the American Medical Association, gathered a group of 11 actuaries in 1914 to form the Casualty Actuarial Society with the goal “to set casualty fire and workers’ compensation insurance on a sound mathematical basis.”[6] Albert Whitney chaired a committee that in 1918 concluded that knowledge or experience about a given employer should be used in conjunction with prior broad industry experience to set an employer’s rate. They called this theory “credibility” and defined the formula we use today with
Credibility = Z
New Rate = Z × experience rate + (1 – Z) × prior rate, where Z = n/(n + K) depends on the number n of observations and K is dependent on the variances of the underlying hypotheses.
In its use of prior experience, the credibility formula was an application of Bayes’ theorem. Credibility became a key tool for casualty actuaries in America, and its use spread to Europe.
Actuaries Overcome the Wrath of R.A. Fisher
While the United States was using Bayes’ theorem for business decisions and France was adapting it for military use, Karl Pearson, founding editor of the journal Biometrika, and R.A. Fisher, known for maximum likelihood testing and randomized design of experiments, were using statistics to show how careful breeding of the British population could produce “supermen and superwomen.” Fisher wrote frequently for Charles Darwin’s son’s journal of the Eugenics Education Society. While Pearson and Fisher feuded for a generation, both displayed great antipathy to anyone promoting Bayesian methods.
Karl’s son, Egon (the Pearson in the famous Neyman-Pearson criteria for hypothesis testing), used Bayesian methods to calculate a host of whimsical probability problems, which he published in 1925. But this enraged both his father and R.A. Fisher. Although he, Neyman, and Fisher collaborated on developing many useful statistical techniques, the latter two maintained an anti-Bayesian attitude.
Meanwhile, in 1924 Émile Borel—a French mathematician known for Borel sets and Borel measures—concluded that one could quantify one’s subjective beliefs by the amount one was willing to bet. He began applying probability to real-world problems in insurance, biology, agriculture, and physics. Almost at the same time an Italian actuary, Bruno de Finetti, suggested that subjective beliefs could be quantified as the “art of guessing.” De Finetti is credited with putting Bayes’ subjectivity on a firm mathematical basis.
In 1928 Arthur Bailey graduated from the University of Michigan after studying statistics and actuarial science. He had been taught that the use of Bayesian priors was “more horrid than spit.”[7] But after many  years of working in the field of pricing workers’ compensation, “He concluded that only a ‘suicidal’ actuary would use Fisher’s method of maximum likelihood, which assigned a zero probability to nonevents. Since many businesses file no insurance claims at all, Fisher’s method would produce premiums too low to cover future losses.”[8]
years of working in the field of pricing workers’ compensation, “He concluded that only a ‘suicidal’ actuary would use Fisher’s method of maximum likelihood, which assigned a zero probability to nonevents. Since many businesses file no insurance claims at all, Fisher’s method would produce premiums too low to cover future losses.”[8]
By 1950 he was ready to present his seminal paper that connected Bayesian theory and credibility, Credibility Procedures—Laplace’s Generalization of Bayes’ Rule and the Combination of Collateral Knowledge With Observed Data. Longley-Cook, the actuary who was asked for the likelihood of a midair collision, used Bailey’s ideas to answer his CEO. Arthur Bailey’s son, Robert, used Bayesian techniques to introduce the idea of merit rating for good drivers. In the 1960s two other actuaries, Hans Bühlmann in Switzerland and Allen Mayerson in the United States, established the firm mathematical basis for Bayesian credibility that actuaries study today.
Nuclear Accidents, Lost Hydrogen Bombs, Breaking the Enigma Code, Cancer and Cigarettes
Beyond actuaries, several other key problem-solvers reinvented Bayesian methods to solve major business, security, and health questions. I say “reinvented” because until 1960 or so, one was considered an outcast if one referred to Bayes’ theorem in one’s work. Sometimes national security issues were cited as the excuse, but often one couldn’t publish work or solutions that involved Bayes’ theorem because the work was considered suspect if it relied on subjective prior distributions. Below are a few interesting examples of these “heretical” applications from McGrayne’s book.
As documented in the movie The Imitation Game, Alan Turing invented a Bayesian method to test short sequences of code that eventually led to decoding messages. U.K. Prime Minister Winston Churchill ordered that all his work and machines be destroyed after the war. Even the existence of the team that worked on the code-busting machine remained classified until 1973. McGrayne’s book goes into quite a bit of detail about breaking the Enigma machine’s code. For example, the movie does not mention the role of the Polish secret service. It held a cryptography class for German-speaking mathematicians. The star student was an actuary named Marián Rejewski who, using intuition and the new mathematics of group theory, determined how the wheels on the Enigma machine were wired. Consequently, by 1938 the Poles were reading 75 percent of the German army’s and air force’s messages.
There were different Enigma codes for the army, air force, and navy. The naval code was the “unbreakable one,” as it required a second encryption that was performed manually according to a secret codebook. To break the navy’s Enigma code, one of these codebooks needed to be seized, and this assignment was given to a certain captain named Ian Fleming—yes, the famous creator of James Bond. After the war, one of Turing’s assistants, Charles Good, continued doing classified analysis and became one of the three top cryptanalysts in Great Britain—and perhaps the world. Good ended his career as a professor at Virginia Polytechnic Institute and State University in Blacksburg, Va., where “at his insistence his contract stipulated that he would always be paid one dollar more than the football coach!”[9]
Nuclear accidents
In the 1950s the United States and the Soviet Union were stockpiling nuclear weapons, and nuclear reactors were being built. There hadn’t been any nuclear accidents, but could the impossible happen? Jacob Bernoulli from the famous family of mathematicians had stated in 1713 that highly improbable events do not happen. The philosopher David Hume agreed. Andrei Kolmogorov, a leading expert in probability theory, argued that if the probability (i.e., the relative frequency) of an event is very small, we can be practically certain the event will not happen in the very next trial. Meanwhile, R.A. Fisher opined that until a nuclear bomb accident occurred, he had no way of judging its future probability.[10] Fortunately, a 23-year-old with a newly acquired Ph.D. did not accept this reasoning.
 General Curtis LeMay (the model for the general in the movie Dr. Strangelove or: How I Learned to Stop Worrying and Love the Bomb) was in charge of the Strategic Air Command, which kept airplanes with nuclear bombs aloft 24/7. He had also helped start RAND Corporation, whose mission it was to use mathematics, statistics, and computers to solve military problems and develop methods of decision-making under conditions of uncertainty. Jimmie Savage was a professor of statistics at the University of Michigan who became a convert to Bayesian methods after visiting Bruno de Finetti. While visiting RAND, he challenged two young associates, Fred Iklé and Albert Madansky, to calculate the probability of an accidental H-bomb explosion. Madansky had financed his graduate studies by working part time for Arthur Bailey, although he did not become an actuary. Madansky did some research and found a list of major accidents involving unarmed nuclear weapons. He concluded that because the “prior” distribution of the probability of an accident was not precisely zero (say, it is 1 in a million), then if there were enough opportunities for an accident (say, 10,000 in the next five years), the probability of an accident becomes significant. As a result of his work, in 1958 he and Iklé were able to convince the hard-nosed LeMay to implement precautionary rules to prevent an inadvertent accident.
General Curtis LeMay (the model for the general in the movie Dr. Strangelove or: How I Learned to Stop Worrying and Love the Bomb) was in charge of the Strategic Air Command, which kept airplanes with nuclear bombs aloft 24/7. He had also helped start RAND Corporation, whose mission it was to use mathematics, statistics, and computers to solve military problems and develop methods of decision-making under conditions of uncertainty. Jimmie Savage was a professor of statistics at the University of Michigan who became a convert to Bayesian methods after visiting Bruno de Finetti. While visiting RAND, he challenged two young associates, Fred Iklé and Albert Madansky, to calculate the probability of an accidental H-bomb explosion. Madansky had financed his graduate studies by working part time for Arthur Bailey, although he did not become an actuary. Madansky did some research and found a list of major accidents involving unarmed nuclear weapons. He concluded that because the “prior” distribution of the probability of an accident was not precisely zero (say, it is 1 in a million), then if there were enough opportunities for an accident (say, 10,000 in the next five years), the probability of an accident becomes significant. As a result of his work, in 1958 he and Iklé were able to convince the hard-nosed LeMay to implement precautionary rules to prevent an inadvertent accident.
Lost hydrogen bomb and a missing submarine
The year was 1966 when four bombs were lost while fueling one of General LeMay’s B-52s. The plane crashed in the Mediterranean Sea near the Palomares fishing village off the coast of Spain. Two of the bombs shattered, spreading plutonium near the village. Another was found on land, but the fourth sank somewhere in the sea and needed to be found quickly—before the Russians found it. John Piña Craven, an applied physicist, was called to the rescue. He was somewhat familiar with Applied Statistical Decision Theory by Robert Schlaifler and Howard Raiffa,[11] which was the first advanced book that used Bayesian methods to solve business problems. After talking to experts, he put forth seven scenarios. He thought that Bayes’ theorem could be used. He hired Wagner Associates, a mathematics firm, to do the analysis.[12] The project was led by a newly minted Ph.D. in probability theory, Tony Richardson. The seabed was divided into a grid with hundreds of cells. Data had to be sent from the command ship by teletype to a land-based, primitive 32K computer to calculate probabilities that the bomb could be in a given cell after each daily search of the seabed. Based on these calculations, Richardson would direct the next day’s search. The bomb was found in a cell near where a fisherman said he saw a large parachute pass over his boat.[13] Two years later, the same firm, Wagner Associates, successfully located a missing nuclear submarine using similar methods.
Lung cancer and heart attacks
 Jerome Cornfield is responsible for the application of Bayes’ theorem to modern medical research.[14] With only a B.A. in history and one course in statistics given by the Department of Agriculture, his work paved the way for cigarette smoking being declared a cause of lung cancer. Thanks to his work, smoking was shown to be one of the four most important risk factors for heart attacks (the others being cholesterol, heart abnormalities, and blood pressure). Cornfield and his wife gave up their 2½-pack-a-day habits, but not so his antagonists Fisher and Neyman. Indeed, Fisher hypothesized that the converse was true: either lung cancer caused one to smoke or hereditary factors led to both smoking and lung cancer.
Jerome Cornfield is responsible for the application of Bayes’ theorem to modern medical research.[14] With only a B.A. in history and one course in statistics given by the Department of Agriculture, his work paved the way for cigarette smoking being declared a cause of lung cancer. Thanks to his work, smoking was shown to be one of the four most important risk factors for heart attacks (the others being cholesterol, heart abnormalities, and blood pressure). Cornfield and his wife gave up their 2½-pack-a-day habits, but not so his antagonists Fisher and Neyman. Indeed, Fisher hypothesized that the converse was true: either lung cancer caused one to smoke or hereditary factors led to both smoking and lung cancer.
In the 1950s most men and an increasing number of women smoked. Studies in 14 different countries showed that a high percentage of lung cancer patients had been smokers. But the studies didn’t prove that smoking caused lung cancer, nor did they tell the public what one’s chances were of getting that fatal disease if one smoked. This quandary offers a perfect application of Bayes’ theorem:
Let P(A) = probability that someone is a heavy smoker and P(B) = probability of having lung cancer. The prior studies give P(A|B), the probability that someone with lung cancer was a smoker. What was desired was P(B|A), the probability of getting lung cancer given that one smoked. By Bayes’ theorem, this probability equals
.
Cornfield’s 1951 paper “stunned the research epidemiologists” and led other researchers to conduct large, prospective studies in England and the United States that tracked populations for three to five years. Both studies clearly showed that heavy smokers were 22 to 24 times more likely to get lung cancer and, surprisingly, suffer heart and circulatory diseases. Because heart disease was more common than lung cancer (and indeed the No. 1 killer in the two countries), Cornfield devised the famous 10-year Framingham study. “Framingham gave him data about two groups of people, those who had died of heart disease and those who had not,” McGrayne says. “Within each group he had information about seven risk factors. Applying Bayes’ theorem, he obtained a posterior probability in the form of a logistic regression function, which he then used to identify the four most important risk factors for cardiovascular disease.”[15]
Cornfield also used Bayes’ theorem in clinical trials because he discovered that Bayesian methods would enable him to reject some hypotheses after only a small number of adverse observations. Frequentists would require the experiment to run to its conclusion so they could gather the statistics needed for their tests of significance. Amazingly, given Cornfield’s prestige (in 1974 he became president of the American Statistical Association) and the fact that he worked at National Institutes of Health (NIH), it would be another 30 years before NIH regularly applied Bayes’ theorem to clinical trials.
Conclusion
Today actuaries use Bayesian analysis all the time. How could we answer my CFO’s question concerning the Ebola risk without making some prior assumptions? How could health actuaries price for the individual health insurance exchanges in 2014 without using all available data to make subjective assumptions? And, of course, credibility is widely used in both pricing and reserving work (see, for example, the January 2014 issue of the Astin Bulletin[16] for a paper titled “Bayesian chain ladder models” for determining incurred but not reported [IBNR] liabilities).
In a 1965 paper, professor Donald Jones, one of the authors of Actuarial Mathematics, summed up the situation between frequentists and Bayesians with the following metaphor. Recall that frequentists need to run tests until they obtain a 95 percent confidence interval. For each statistical test, the frequentist has a different “box.” Jones writes,
“Each of his boxes has an intake hole at the top for the experimental data and an output hole at the right end. There is a warning on each box which says: ‘Use seriously only with k units or more of input.’ He would then offer you any of his boxes. … The Bayesian has only one black box—but it has three holes: an additional intake hold on the left for experience, information, and prior opinion. I think actuaries should be among the most ardent welcomers and users of the Bayesians’ one black box. In all their work and training actuaries emphasize that decisions are based on the data and judgment, but classical theories of statistics have never offered a place for, or required, a well-defined judgment factor.”[17]
It has been over 50 years since professor Jones made this observation. Bayesian analysis is much more accepted today because (1) it has been shown to work, repeatedly, and (2) there is a firm mathematical basis for the theory and applications. Computer software programs today apply Bayesian theory to enable computers to “learn” and “make decisions,” such as translating a Wikipedia article from English to Croatian. It is thought that the brain uses Bayesian techniques to filter the hundreds of megabits of sensory information that it receives every second.[18]
Over the last 150 years actuaries have been inventing or adapting the latest techniques to make better judgments based on the data at hand. We should be proud of the role actuaries have played in promoting the use of Bayesian thinking. Let us continue to stay on the cutting edge in order to better serve all our stakeholders. ■
BY ROY GOLDMAN
ROY GOLDMAN, MAAA, FSA, CERA, is a retired actuary living in Jacksonville Beach, Fla.
Endnotes
[1] In 1982 Connecticut General Life Insurance Co CG purchased INA, the first U.S. stock insurer, to form Cigna.
[2] E.J. Moorhead; Our Yesterdays: the History of the Actuarial Profession in North America 1809-1979; p. 384.
[3] The full title: Observations on Reversionary Payments: On Schemes for Providing Annuities for Widows, and for Persons in Old Age: On the Method of Calculating the Values of Assurances on Lives: and on the National Debt.
[4] S.B. McGrayne; The Theory That Would Not Die; p. 30.
[5] Ibid.; p. 33.
[6] Ibid.; p. 43.
[7] This quote is attributed by the author to Charles Hewitt, a well-known casualty actuary. She also quotes Hewitt as referring to Bailey as “the da Vinci or a Michelangelo” to the few actuaries who understood his work.
[8] McGrayne op. cit.; p. 92.
[9] Ibid.; p. 100.
[10] Ibid.; p. 121.
[11] Howard Raiffa was told in the late 1940s that because he was Jewish, he would be discriminated against as an engineer or scientist. Because he had experienced discrimination in the army and in housing, he believed what he was told. According to McGrayne, “Then he learned that insurance actuaries were graded on objective, competitive examinations. Seeking a field where competence counted more than religion, Raiffa enrolled in the University of Michigan’s actuarial program, where Arthur Bailey had studied.”
[12] McGrayne writes that Daniel Wagner was so absent-minded that his car once ran out of gas three times in a single day.
[13] On June 20, 2016, the New York Times reported that the United States and Spain are still arguing over how to best clean up the site. At the time, Spaniards and naval crewmen were mistakenly told that there was no danger from radiation.
[14] In 1933 Cornfield began his career in the Department of Labor because that was the one department that would hire Jews. The author’s vignettes of Cornfield and all the other major researchers make the book fun to read. They are all idiosyncratic; some, like Fisher, are very cruel and crude people, but all are unbelievably driven.
[15] McGrayne op. cit.; p. 115.
[16] The Journal of the International Actuarial Association.
[17] Transactions of the Society of Actuaries; vol. 17; p. 33; as quoted by Moorhead, op. cit.
[18] McGrayne op. cit.; p. 247–249.





